Câu hỏi/bài tập:
Biển quảng cáo của một quán cà phê được treo cân bằng nhờ một dây nằm ngang và dây còn lại hợp với trần một góc \(\alpha \) như Hình 14.6.
a. Giữ cho một dây luôn căng và có phương nằm ngang, thay đổi vị trí và độ dài dây treo trên trần. Xác định điều kiện góc \(\alpha \)để hệ có thể cân bằng.
b. Biển quảng cáo có trọng lượng là P, tính lực căng trên hai dây treo.

Vận dụng kiến thức về điều kiện cân bằng của một vật.

Advertisements (Quảng cáo)
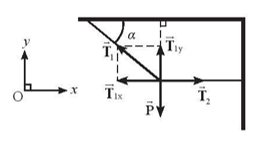
a) Điểm treo chịu tác dụng của trọng lực \(\overrightarrow P \) hướng thẳng đứng xuống, lực căng dây \(\overrightarrow {{T_1}} \) và \(\overrightarrow {{T_2}} \)
Để hệ cân bằng thì: \(\overrightarrow P + \overrightarrow {{T_1}} + \overrightarrow {{T_2}} = \overrightarrow 0 \). Ta thấy:
Trên phương Oy, thành phần trọng lực \(\overrightarrow P \) hướng xuống luôn cân bằng với thành phần \(\overrightarrow {{T_{1y}}} \) hướng lên.
Trên phương Ox, lực căng dây \(\overrightarrow {{T_2}} \) luôn căng và có phương nằm ngang nên thành phần \(\overrightarrow {{T_{1x}}} \) phải hướng theo chiều âm của trục Ox.
Do đó, góc \(\alpha \)phải thỏa mãn điều kiện: \({0^0} < \alpha < {90^0}\).
b) Áp dụng điều kiện cân bằng của hệ: \(\overrightarrow P + \overrightarrow {{T_1}} + \overrightarrow {{T_2}} = \overrightarrow 0 \,\left( * \right)\)
Chiếu (*) lên Ox và Oy ta có: \(\left\{ \begin{array}{l}{T_1}.\sin \alpha = P\\{T_1}.\cos \alpha = {T_2}\end{array} \right.\)
Vậy \({T_1} = \frac{P}{{\sin \alpha }}\) và \({T_2} = \frac{P}{{\tan \alpha }}\).
