Bài 33. Biến dạng của vật rắn trang 64, 65 SBT Vật lý 10 Kết nối tri thức: Vật cấu tạo từ chất nào sau đây sẽ không có tính đàn hồi?...

33.1

Vật cấu tạo từ chất nào sau đây sẽ không có tính đàn hồi?

A. Sắt. B. Đồng. C. Nhôm. D. Đất sét.

Kiến thức về biến dạng đàn hồi.

Khi có tác dụng của ngoại lực, vật rắn sẽ bị biến dạng.

Khi không còn tác dụng của ngoại lực, nếu vật rắn lấy lại được hình dạng và kích thước ban đầu thì biến dạng của vật là biến dạng đàn hồi. Vật có khả năng biến dạng đàn hồi thì có tính đàn hồi. Trong các vật cấu tạo từ các chất phía trên thì chỉ có đất sét là không có tính đàn hồi.

Chọn đáp án D.

33.2

Một lò xo có độ cứng 80 N/m được treo thẳng đứng. Khi móc vào đầu tự do của nó một vật có khối lượng 400 g thị lò xo dài 18 cm. Hỏi khi chưa móc vật thì lò xo dài bao nhiêu? Lấy g = 10 m/s².

A. 17,5 cm. B. 13 cm. C. 23 cm. D. 18,5 cm.

Vật nặng chịu tác dụng của lực đàn hồi và trọng lực: F_dh = P ↔ k.∆l = mg.

Vật nặng chịu tác dụng của lực đàn hồi và trọng lực: F_dh = P ↔ k.∆l = mg.

=> ∆l = l – l₀ = \(\frac{{mg}}{k}\)= \(\frac{{0,4.10}}{{80}}\)= 0,05 m = 5 cm

=> l₀ = 18 – 5 = 13 cm.

Vậy khi chưa móc vật thì lò xo dài 13 cm.

Chọn đáp án B.

33.3

Phát biểu nào sau đây là sai khi nói về đặc điểm của lực đàn hồi?

A. Lực đàn hồi xuất hiện khi vật có tính đàn hồi bị biến dạng.

B. Trong giới hạn đàn hồi, khi độ biến dạng của vật càng lớn thì lực đàn hồi cũng càng lớn.

C. Lực đàn hồi có chiều cùng với chiều của lực gây biến dạng.

D. Lực đàn hồi luôn ngược chiều với chiều của lực gây biến dạng.

Nắm vững lý thuyết về lực đàn hồi.

A lực đàn hồi xuất hiện khi vật có tính đàn hồi bị biến dạng là đúng. Ví dụ khi ta nén hoặc kéo hai đầu lò xo. Các lực này ngược chiều với lực tay tác dụng vào lò xo và được gọi là lực đàn hồi của lò xo.

B đúng vì độ lớn lực đàn hồi được tính bằng công thức: F_đh = k.∆l (trong đó ∆l là độ biến dạng của vật).

C sai, D đúng vì lực đàn hồi chống lại nguyên nhân làm nó biến dạng và có xu hướng đưa nó về hình dạng và kích thước ban đầu nên lực đàn hồi sẽ ngược chiều với chiều của lực gây biến dạng.

Chọn đáp án C.

33.4

Hai lò xo cùng chiều dài tự nhiên, có độ cứng lần lượt là k₁ = 40 N/m và

k₂ = 60 N/m. Hỏi nếu ghép song song hai lò xo thì độ cứng tương đương là bao nhiêu?

A. 100 N/m. B. 240 N/m. C. 60 N/m. D. 30 N/m

Hai lò xo ghép song song thì: k = k₁ + k₂.

Hai lò xo ghép song song nên: k = k₁ + k₂ = 40 + 60 = 100 N/m.

Chọn đáp án A.

33.5

Hai lò xo cùng chiều dài tự nhiên, có độ cứng lần lượt là k₁ = 40 N/m và k₂ = 60 N/m. Hỏi nếu ghép nối tiếp hai lò xo thì độ cứng tương đương là bao nhiêu?

A. 20 N/m. B. 24 N/m. C. 100 N/m. D. 2 400 N/m.

Hai lò xo ghép nối tiếp, ta có công thức: \(\frac{1}{k} = \frac{1}{{{k_1}}} + \frac{1}{{{k_2}}}\).

Vì hai lò xo ghép nối tiếp nên ta có công thức: \(\frac{1}{k} = \frac{1}{{{k_1}}} + \frac{1}{{{k_2}}}\).

=> k = \(\frac{{{k_1}.{k_2}}}{{{k_1} + {k_2}}}\) = \(\frac{{40.60}}{{40 + 60}}\)= 24 N/m.

Chọn đáp án B.

33.6

Một lò xo có chiều dài 1₁, khi chịu lực kéo F₁ và có chiều dài 1₂ khi chịu lực

kéo F₂. Chiều dài tự nhiên của lò xo bằng

A. \(\frac{{{F_2}{I_1} + {F_1}{I_2}}}{{{F_1} + {F_2}}}\)

B.\(\frac{{{F_2}{I_1} - {F_1}{I_2}}}{{{F_1} - {F_2}}}\)

C. \(\frac{{{F_2}{I_1} - {F_1}{I_2}}}{{{F_1} + {F_2}}}\)

D. \(\frac{{{F_2}{I_1} + {F_1}{I_2}}}{{{F_1} - {F_2}}}\)

Áp dụng định luật Hooke: F = k.∆l = k(l – l₀).

Áp dụng định luật Hooke: F = k.∆l = k(l – l₀).

Ta có: F₁ = k(l₁ – l₀). (1)

F₂ = k(l₂ – l₀). (2)

Chia vế với vế của (1) cho (2) ta được: \(\frac{{{F_1}}}{{{F_2}}} = \frac{{{l_1} - {l_0}}}{{{l_2} - {l_0}}}\)=> (F₂ – F₁)l₀ = \({F_2}{l_1} - {F_1}{l_2}\)

=> l₀ = \(\frac{{{F_2}{l_1} - {F_1}{l_2}}}{{{F_2}-{\rm{ }}{F_1}}}\).

Chọn đáp án B.

33.7

Một lò xo có chiều dài tự nhiên là lo. Treo lò xo thẳng đứng và móc vào đầu dưới một vật khối lượng m₁ = 100 g thì chiều dài lò xo bằng 31 cm. Treo thêm vào đầu dưới một vật nữa có khối lượng m₂ = 100 g thì chiều dài lò xo bằng 32 cm. Lấy g = 10 m/s². Tìm độ cứng và chiều dài tự nhiên của lò xo.

Vật nặng chịu tác dụng của lực đàn hồi và trọng lực: F_dh = P ↔ k.∆l = mg.

Vật nặng chịu tác dụng của lực đàn hồi và trọng lực: F_dh = P ↔ k.∆l = mg

Khi chỉ có vật m₁: m₁g = k(l₁ – l₀) (1)

Khi treo cả hai vật: (m₁ + m₂)g = k(l₂ – l₀) (2)

Chia vế với vế của (1) cho (2) ta được: \(\frac{{{m_1}}}{{{m_1} + {m_2}}} = \frac{{{l_1} - {l_0}}}{{{l_2} - {l_0}}}\)

=> m₂.l₀ = \(({m_1} + {m_2}){l_1} - {m_1}{l_2}\)

=> l₀ = \(\frac{{({m_1} + {m_2}){l_1} - {m_1}{l_2}}}{{{m_2}}}\)= \(\frac{{(0,1 + 0,1).0,31 - 0,1.0,32}}{{0,1}}\)= 0,3 m.

Thay váo (1) ta tính được k = \(\frac{{{m_1}g}}{{{l_1} - {l_0}}}\)= \(\frac{{0,1.10}}{{0,31 - 0,3}}\)= 100 N/m.

33.8

Một súng lò xo gồm lò xo chiều dài tự nhiên 200 mm, độ cứng k = 2 000 N/m và đạn có khối lượng m = 50 g. Ban đầu lò xo bị nén đến chiều dài 50 mm (Hình 33.1). Hãy tính tốc độ của viên đạn khi bắn ra khỏi nòng súng.

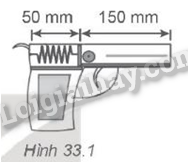
Áp dụng định luật bảo toàn cơ năng:

Trong đó: W = W_t + W_đ = \(\frac{1}{2}k{x^2} + \frac{1}{2}m{v^2}\).

Ban đầu lò xo bị nén, thế năng đàn hồi dự trữ trong lò xo bằng W = \(\frac{1}{2}k{x^2}\).

Khi bắn, thế năng đàn hồi cuae lò xo sẽ chuyển hóa thành động năng và truyền cho viên đạn: W_đ = \(\frac{1}{2}m{v^2}\).

Áp dụng định luật bảo toàn năng lượng, ta có: \(\frac{1}{2}k{x^2}\)= \(\frac{1}{2}m{v^2}\)

=> v = x\(\sqrt {\frac{k}{m}} \)= 0,15.\(\sqrt {\frac{{2000}}{{0,05}}} \)= 30 m/s.