Câu hỏi/bài tập:
4.16. Đặt hiệu điện thế 6 V vào hai đầu điện trở 3 Ω. Cường độ dòng điện chạy qua điện trở là
A. 0,5 A.
B. 6 A.
C. 2 A.
D. 3 A.

Vận dụng kiến thức đã học về cường độ dòng điện qua một vật dẫn kim loại: \(I = \frac{U}{R}\)

Cường độ dòng điện chạy qua điện trở là:
\(I = \frac{U}{R} = \frac{6}{3} = 2{\rm{ A}}\)
Đáp án: C. 2 A.
4.17. Đặt một hiệu điện thế 12 V vào giữa hai đầu một điện trở 4,0 Ω thì lượng điện tích chạy qua điện trở trong mỗi giây là
A. 3 C.
B. 4 C.
C. 12 C.
D. 48 C.

Vận dụng kiến thức đã học về cường độ dòng điện:
- Cường độ dòng điện: \(I = \frac{{\Delta q}}{{\Delta t}}\)
- Cường độ dòng điện qua một vật dẫn kim loại: \(I = \frac{U}{R}\)

Lượng điện tích chạy qua điện trở trong mỗi giây là:
\(\Delta q = I\Delta t = \frac{U}{R}\Delta t = \frac{{12}}{4}.1 = 3{\rm{ C}}\)
Đáp án: A. 3 C.
4.18. Ở Hình 4.3, khi hiệu điện thế U tăng, phát biểu nào sau đây đúng?
A. Điện trở của diode tăng.
B. Điện trở của dây kim loại giảm.
C. Điện trở của diode giảm.
D. Điện trở của dây kim loại tăng.
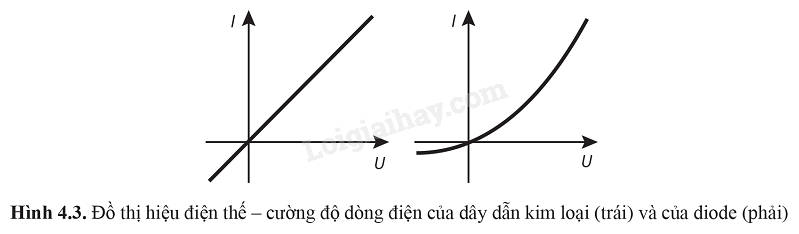

Vận dụng kiến thức đã học về điện trở và cách đọc đồ thị.
- Điện trở: \(R = \frac{U}{I}\)

Đáp án: C. Điện trở của diode giảm.
4.19. Một dây dẫn kim loại có điện trở R được cắt thành ba đoạn bằng nhau rồi tết lại với nhau để tạo thành một dây dẫn mới có chiều dài bằng 1/3 chiều dài ban đầu. Điện trở của dây mới này có giá trị là
A. 3R.
B. R/9.
C. R/3.
D. 9R.

Vận dụng kiến thức đã học về điện trở trong dây dẫn: \(R = \rho \frac{l}{S}\)

Ta có: \(l’ = \frac{1}{3}l;{\rm{ }}S’ = 3S{\rm{; }}R = \rho \frac{l}{S}\)
\( \Rightarrow R’ = \rho \frac{{l’}}{{S’}} = \rho \frac{l}{{3.3S}} = \frac{R}{9}\)
Đáp án: B. R/9.
4.20. Cho mạch điện (Hình 4.4), các điện trở R đều bằng nhau. Điện trở tương đương giữa M và N là
A. R/2.
B. R.
C. 2R.
D. 4R.
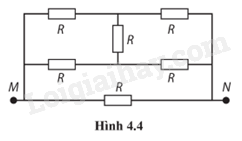

Vận dụng kiến thức đã học về mạch điện:
- Mạch cầu: khi \(\frac{{{R_1}}}{{{R_3}}} = \frac{{{R_2}}}{{{R_4}}}\) thì sơ đồ mạch được vẽ lại: (R1ntR2)//(R3ntE4)//R
- Điện trở song song: \(\frac{1}{R} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + ... + \frac{1}{{{R_n}}}\)
- Điện trở nối tiếp: R = R1 + R2 + … + Rn

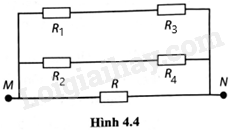
Vì \(\frac{{{R_1}}}{{{R_3}}} = \frac{{{R_2}}}{{{R_4}}} = 1\) nên mạch điện được vẽ lại như hình bên.
Sơ đồ mạch: (R1ntR2)//(R3ntE4)//R
\(\begin{array}{l}\frac{1}{{{R_{MN}}}} = \frac{1}{{{R_{13}}}} + \frac{1}{{{R_{24}}}} + \frac{1}{R} = \frac{1}{{{R_1} + {R_3}}} + \frac{1}{{{R_2} + {R_4}}} + \frac{1}{R} = \frac{1}{{R + R}} + \frac{1}{{R + R}} + \frac{1}{R} = \frac{2}{R}\\ \Rightarrow {R_{MN}} = \frac{R}{2}\end{array}\)
4.21. Cường độ dòng điện đi qua một vật dẫn là 6,3 A khi hiệu điện thế giữa hai đầu vật dẫn là 12 V. Tính điện trở của vật dẫn.

Vận dụng kiến thức đã học về điện trở của vật dẫn: \(R = \frac{U}{I}\)

Điện trở của vật dẫn là:
\(R = \frac{U}{I} = \frac{{12}}{{6,3}} = 1,9{\rm{ }}\Omega \)
4.22. Đồ thị I – U của một vật dẫn được biểu diễn ở Hình 4.5. a) Từ đồ thị có thể suy ra định luật nào biểu diễn mối liên hệ giữa I và U? b) Tính điện trở của vật dẫn này.
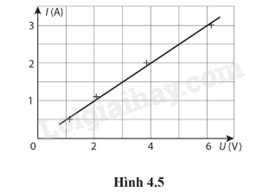

Vận dụng kiến thức đã học về:
- Định luật Ohm: cường độ dòng điện đi qua 2 điểm của một vật dẫn điện luôn có tỷ lệ thuận với hiệu điện thế đi qua 2 điểm đó, và cường độ dòng điện tỷ lệ nghịch với điện trở của dây dẫn.
- Điện trở của vật dẫn: \(R = \frac{U}{I}\)

a) Từ đồ thị có thể suy ra định luật Ohm.
b) Điện trở của vật dẫn là:
\(R = \frac{U}{I} = \frac{2}{1} = 2{\rm{ }}\Omega \)
4.23. Cho mạch điện (Hình 4.6). Hiệu điện thế U = 12 V, điện trở các dây nối không đáng kể. Tìm số chỉ của các vôn kế.
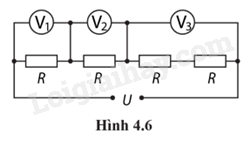

Vận dụng kiến thức đã học về mạch điện:
- Điện trở nối tiếp: R = R1 + R2 + … + Rn; U = U1 + U2 + … + Un;I = I1=I2= … = In.
- Điện trở của vật dẫn: \(R = \frac{U}{I}\)

Điện trở tương đương của mạch điện này là:
\({R_{td}} = R + R + R + R = 4R\)
Cường độ dòng điện trong mạch là:
\(I = \frac{U}{{{R_{td}}}} = \frac{{12}}{{4{\rm{R}}}} = \frac{3}{R}{\rm{ A}}\)
Số chỉ vôn kế 1 và 2:
\({V_1} = IR = {V_2} = \frac{3}{R}R = 3{\rm{ V}}\)
Advertisements (Quảng cáo)
Số chỉ vôn kế 3:
\({V_3} = I\left( {R + R} \right) = \frac{3}{R}.2R = 6{\rm{ V}}\)
4.24. Khi hiệu điện thế giữa hai đầu LED là 2,0 V thì cường độ dòng điện đi qua nó là 20 mA.
Tính điện trở của LED.

Vận dụng kiến thức đã học về điện trở của vật dẫn: \(R = \frac{U}{I}\)

Điện trở của LED là:
\(R = \frac{U}{I} = \frac{2}{{{{20.10}^{ - 3}}}} = 100{\rm{ }}\Omega \)
4.25. Bảng sau đây là các giá trị của cường độ dòng điện I qua một điện trở tương ứng với các hiệu điện thế khác nhau U giữa hai đầu của nó.
|
U (V) |
0 |
0,19 |
0,48 |
1,47 |
2,92 |
4,56 |
6,56 |
8,70 |
|
I (A) |
0 |
0,20 |
0,4 |
0,60 |
0,80 |
1,00 |
1,20 |
1,40 |
a) Tính giá trị của điện trở ứng với mỗi giá trị cường độ dòng điện và hiệu điện thế. b) Vẽ đồ thị biểu diễn sự biến thiên của điện trở theo cường độ dòng điện.

Vận dụng kiến thức đã học về điện trở của vật dẫn: \(R = \frac{U}{I}\)

a)
|
I (A) |
0,20 |
0,4 |
0,60 |
0,80 |
1,00 |
1,20 |
1,40 |
|
R (Ω) |
0,95 |
1,2 |
2,45 |
3,65 |
4,56 |
5,47 |
6,21 |
b)
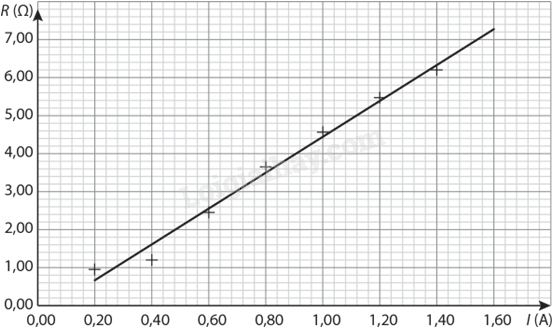
4.26. Cho mạch điện (Hình 4.7). U1 = 10 V; R1 = 10 Ω.
Khi biến trở R2 thay đổi giá trị từ 0 V đến 40 V, xác định khoảng giá trị của hiệu điện thế U2.


Vận dụng kiến thức đã học về mạch điện:
- Điện trở của vật dẫn: \(R = \frac{U}{I}\)
- Điện trở nối tiếp: R = R1 + R2 + … + Rn; U = U1 + U2 + … + Un;I = I1=I2= … =In.

Khi R2 = 0; U2 = 0
Khi R2 = 40 Ω;
\(\begin{array}{l}I = \frac{U}{R} = \frac{{{U_1}}}{{{R_1} + {R_2}}} = \frac{{10}}{{10 + 40}} = 0,2{\rm{ A; }}\\{U_2} = IR = 0,2.40 = 8{\rm{ V}}\end{array}\)
4.27. Khi hiệu điện thế giữa hai đầu của một vật dẫn là 2,00 V, cường độ dòng điện qua nó là 10,0 mA. Khi hiệu điện thế là 8,00 V, cường độ dòng điện là 60,0 mA.a) Tính điện trở của vật dẫn ứng với hiệu điện thế 2,0 V và 8,0 V.b) Vật dẫn này có tuân theo định luật Ohm không?

Vận dụng kiến thức đã học về:
- Định luật Ohm: cường độ dòng điện đi qua 2 điểm của một vật dẫn điện luôn có tỷ lệ thuận với hiệu điện thế đi qua 2 điểm đó, và cường độ dòng điện tỷ lệ nghịch với điện trở của dây dẫn.
- Điện trở của vật dẫn: \(R = \frac{U}{I}\)

a) Điện trở của vật dẫn:
Khi U = 2 V ; \(R = \frac{U}{I} = \frac{2}{{{{10.10}^{ - 3}}}} = 200{\rm{ }}\Omega {\rm{ }}\)
Khi U = 8 V ; \(R = \frac{U}{I} = \frac{8}{{{{60.10}^{ - 3}}}} = 133{\rm{ }}\Omega {\rm{ }}\)
b) Vì điện trở của vật dẫn thay đổi khi thay đổi cường độ dòng điện và hiệu điện thế nên vật dẫn này không tuân theo định luật Ohm.
4.28. Cho mạch điện (Hình 4.8). NTC là điện trở nhiệt ngược. R1 = 5,0 Ω; R2 = 6,4 Ω. Bỏ qua điện trở của ampe kế và dây nối.
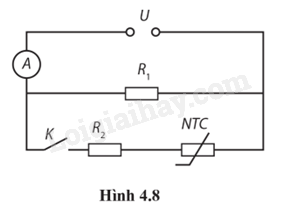
Khi ngắt công tắc K, ampe kế A chỉ 0,48 A.Khi đóng công tắc K, ampe kế A chỉ 0,72 Aa) Tính hiệu điện thế U.b) Tính điện trở của điện trở nhiệt.c) Khi tăng nhiệt độ của điện trở nhiệt, số chỉ của ampe kế tăng hay giảm? Vì sao?

Vận dụng kiến thức đã học về mạch điện:
- Định luật Ohm: cường độ dòng điện đi qua 2 điểm của một vật dẫn điện luôn có tỷ lệ thuận với hiệu điện thế đi qua 2 điểm đó, và cường độ dòng điện tỷ lệ nghịch với điện trở của dây dẫn.
- Điện trở của vật dẫn: \(R = \frac{U}{I}\)
- Điện trở song song: \(\frac{1}{R} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + ... + \frac{1}{{{R_n}}}\); I = I1 + I2 + … + In ; U = U1 = U2 = … = Un
- Điện trở nối tiếp: R = R1 + R2 + … + Rn; U = U1 + U2 + … + Un;I = I1=I2= … = In
- Khi tăng nhiệt độ của điện trở nhiệt, điện trở của điện trở nhiệt giảm.

a) Hiệu điện thế \(U = I{R_1} = 0,48.5 = 2,4{\rm{ V}}\)
b) Khi đóng công tắc K.
Điện trở tương đương của mạch là:
\({R_b} = \frac{U}{I} = \frac{{2,4}}{{0,72}} = 3,3{\rm{ }}\Omega {\rm{ }}\)
Mà \(\frac{1}{{{R_b}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_{2NTC}}}}\)
\(\begin{array}{l}\frac{1}{{{R_b}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_{2NTC}}}}\\ \Rightarrow \frac{1}{{{R_{2NTC}}}} = \frac{1}{{{R_b}}} - \frac{1}{{{R_1}}} = \frac{1}{{3,3}} - \frac{1}{5} = \frac{1}{{10}}\\ \Rightarrow {R_{2NTC}} = 10{\rm{ }}\Omega \\{R_{2NTC}} = {R_2} + {R_{NTC}}\\ \Rightarrow {R_{NTC}} = {R_{2NTC}} - {R_2} = 10 - 6,4 = 3,6{\rm{ }}\Omega \end{array}\)
Vậy điện trở của điện trở nhiệt là \({R_{NTC}} = 3,6{\rm{ }}\Omega \)
c) Điện trở của điện trở nhiệt giảm nên điện trở toàn mạch giảm và số chỉ của ampe kế tăng.
