Trắc nghiệm
19.1
Đề bài:
Đặt hiệu điện thế 12 V vào hai đầu đoạn mạch. Năng lượng điện mà đoạn mạch đã tiêu thụ khi có điện lượng 150 C chuyển qua mạch bằng
A. 1800 J.
B. 12,5 J.
C. 170 J.
D. 138 J.
Phương pháp giải
Vận dụng công thức tính năng lượng tiêu thụ

A=qU=150.12=1800J
Đáp án A
19.2
Đề bài:
Đặt một hiệu điện thế không đổi vào hai đầu một biến trở R. Điều chỉnh giá trị R và đo công suất toả nhiệt P trên biến trở. Chọn phát biểu đúng.
A. P tỉ lệ với R.
B. P tỉ lệ với R2.
C. P tỉ lệ nghịch với R.
D. P tỉ lệ nghịch với R2.
Phương pháp giải
Vận dụng mối quan hệ giữa công suất và điện trở

Công suất \({\rm{P}} = \frac{{{U^2}}}{R}\)
Đáp án C
19.3
Đề bài:
Đặt hiệu điện thế U vào hai đầu một điện trở. Khi có điện lượng q chuyển qua điện trở thì năng lượng điện tiêu thụ A của điện trở được xác định bằng công thức A=qU. Chọn phát biểu đúng.
A. Năng lượng điện tiêu thụ của điện trở không phụ thuộc vào giá trị điện trở.
B. Năng lượng điện tiêu thụ của điện trở phụ thuộc vào giá trị điện trở.
C. Hiệu điện thế U giữa hai đầu điện trở tỉ lệ nghịch với điện lượng q chuyển qua điện trở.
D. Hiệu điện thế U giữa hai đầu điện trở tỉ lệ thuận với điện lượng q chuyển qua điện trở.
Phương pháp giải
Vận dụng lý thuyết vào công thức đã cho

Với U cho trước và khi có điện lượng q chuyển qua thì năng lượng tiêu thụ là A=qU. Giá trị điện trở R càng lớn thì dòng điện càng nhỏ, như thế sẽ cần thời gian lâu hơn để điện lượng là q và ngược lại nhưng hoàn toàn không ảnh hưởng đến giá trị năng lượng tiêu thụ A. Tóm lại, với một hiệu điện thế cho trước xác định năng lượng tiêu thụ điện của một đoạn mạch chỉ còn phụ thuộc vào điện lượng chuyển qua mạch theo công thức A=qU
19.4
Đề bài:
Mắc hai đầu một biến trở vào hai cực của một nguồn điện có suất điện động E. Điều chỉnh biến trở và đo độ lớn hiệu điện thế giữa hai cực nguồn điện U. Chọn phát biểu đúng.
A. Tỉ số \(\frac{U}{{\rm{E}}}\) càng lớn nếu giá trị biến trở càng lớn.
B. Tỉ số \(\frac{U}{{\rm{E}}}\)càng lớn nếu giá trị biến trở càng nhỏ.
C. Hiệu (E−U) không đổi khi giá trị biến trở thay đổi.
D. Tổng (E+U) không đổi khi giá trị biến trở thay đổi.
Phương pháp giải
Tính tỉ số \(\frac{U}{{\rm{E}}}\)

Tỉ số: \(\frac{U}{{\rm{E}}} = \frac{R}{{R + r}} = \frac{1}{{1 + \frac{r}{R}}}\)⇒R càng lớn thì \(\frac{U}{{\rm{E}}}\)càng lớn.
19.5
Đề bài:
Mắc hai đầu một điện trở R vào hai cực của một acquy. Sau một khoảng thời gian, tổng năng lượng mà acquy cung cấp là 10 J, trong đó nhiệt lượng toả ra trên điện trở là 8,5 J. Chọn đáp án đúng.
A. Điện trở trong của acquy bằng 0 .
B. Điện trở trong của acquy lớn hơn R.
C. Điện trở trong của acquy nhỏ hơn R.
D. Hiệu suất của acquy bằng 15%.
Phương pháp giải
Tính nhiệt lượng tỏa ra

Năng lượng acquy cung cấp bằng tổng năng lượng toả nhiệt trên điện trở R và nhiệt lượng toả ra bên trong acquy (do có điện trở trong r).
Suy ra: Nhiệt lượng toả ra trong nguồn bằng: 10−8,5=1,5 J
Vì cùng dòng điện nên r
19.6
Đề bài:
Mắc hai đầu biến trở vào hai cực của một bình acquy. Điều chỉnh để giá trị của biến trở thay đổi từ 0 đến rất lớn. Chọn phát biểu đúng.
A. Công suất toả nhiệt trên biến trở luôn tăng.
B. Công suất toả nhiệt trên biến trở luôn giảm.
C. Công suất toả nhiệt trên biến trở giảm rồi tăng.
D. Công suất toả nhiệt trên biến trở tăng rồi giảm.
Phương pháp giải
Dựa vào công suất tỏa nhiệt

Công suất toả nhiệt P trên biến trở phụ thuộc vào giá trị biến trở R:
\({\rm{P}} = R{I^2} = R{\left( {\frac{{\rm{E}}}{{R + r}}} \right)^2} = \frac{{{{\rm{E}}^2}}}{{R + \frac{{{r^2}}}{R} + 2r}}\)⇒Khi R tăng từ 0 thì P sẽ tăng từ 0 và đạt cực đại khi R = r, nếu sau đó tiếp tục tăng R đến rất lớn thì P giảm dần về 0 .
19.7
Đề bài:
Mắc hai đầu biến trở vào hai cực của một bình acquy. Điều chỉnh biến trở và đo công suất toả nhiệt P trên biến trở thì thấy kết quả là P có cùng giá trị tương ứng với hai giá trị của biến trở là 2Ω và 8Ω. Điện trở trong của acquy bằng
A. 2Ω.
B. 4Ω.
C. 6Ω.
D. 8Ω.
Phương pháp giải
Advertisements (Quảng cáo)
Dựa vào công suất tỏa nhiệt suy ra phương trình bậc 2 của R để giải

Công suất toả nhiệt trên biến trở: \({\rm{P}} = R{I^2} = R{\left( {\frac{{\rm{E}}}{{R + r}}} \right)^2} \Rightarrow {R^2} - \left( {\frac{{{{\rm{E}}^2}}}{{\rm{P}}} - 2r} \right)R + {r^2} = 0\left( 1 \right)\)
Với mỗi giá trị P xác định thì (1) là một phương trình bậc 2 theo R. Theo đề bài, có hai giá trị khác nhau của biến trở R1 và R2 ứng với cùng một công suất P nghĩa là R1 và R2 là hai nghiệm của (1) thoả định lý Viète (Vi-et): \({R_1}{R_2} = {r^2} \Rightarrow r = \sqrt {{R_1}{R_2}} = \sqrt {2.8} = 4{\rm{\Omega }}\)
Tự luận
19.1
Đề bài:
Đặt hai đầu điện trở R vào một hiệu điện thế U thì dòng điện chạy qua điện trở là I. Công suất toả nhiệt trên điện trở có thể xác định bằng công thức: P=RI2 và \({\rm{P}} = \frac{{{U^2}}}{R}\) . Công thức P=RI2 cho thấy R càng tăng thì P càng tăng, còn công thức \({\rm{P}} = \frac{{{U^2}}}{R}\) lại cho thấy R càng tăng thì P càng giảm. Như vậy, liệu rằng hai công thức này có mâu thuẫn với nhau hay không? Giải thích
Phương pháp giải
Dựa vào mối liên hệ giữa U, I, R

Không mâu thuẫn. Công thức P=RI2 chỉ cho kết quả P tỉ lệ thuận với R nếu duy trì dòng điện I qua nó là không đổi. Tương tự, công thức \({\rm{P}} = \frac{{{U^2}}}{R}\)chỉ cho kết quả P tỉ lệ nghịch với R khi hiệu điện thế U giữa hai đầu điện trở được duy trì không đổi. Trong khi hiệu điện thế U và cường độ dòng điện I có mối liên hệ với nhau qua định luật Ohm.
19.2
Đề bài:
Mắc hai đầu một điện trở R vào hai cực của một nguồn điện có suất điện động E và điện trở trong r. Gọi P là công suất tiêu thụ ở mạch ngoài và P0 là công suất phát ra của nguồn. Hiệu suất của nguồn điện được xác định bằng tỉ số: \(H = \frac{{\rm{P}}}{{{{\rm{P}}_0}}}\) . Chứng minh rằng trong trường hợp mạch điện trên, có thể biểu diễn: \(H = \frac{R}{{R + r}}\)
Phương pháp giải
Dựa vào công thức tính công suất

Ta có:\(H = \frac{{\rm{P}}}{{{{\rm{P}}_0}}} = \frac{{UI}}{{{\rm{E}}I}} = \frac{U}{{\rm{E}}}\)với \(I = \frac{{\rm{E}}}{{R + r}} \Rightarrow U = RI = \frac{{R{\rm{E}}}}{{R + r}} \Rightarrow \frac{U}{{\rm{E}}} = \frac{R}{{R + r}}\)
19.3
Đề bài:
Cho mạch điện như Hình 19.1. Suất điện động E của nguồn chưa biết. Bỏ qua điện trở của các dây nối. Tìm giá trị của E để nguồn 10 V được nạp điện.
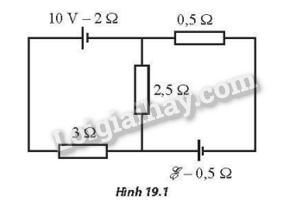
Phương pháp giải
Áp dụng định luật Ohm cho toàn mạch

Nguồn 10 V được nạp khi E có giá trị đủ lớn để triệt tiêu dòng điện do nguồn 10 V tạo ra. Nghĩa là dòng điện chạy qua nguồn 10 V bằng 0 . Khi đó hiệu điện thế giữa hai đầu điện trở 2,5Ω bằng 10 V. Suy ra dòng điện chạy do nguồn phát bằng 4 A. Từ đó, định luật Ohm cho toàn mạch kín: \(4 = \frac{{\rm{E}}}{{3,5}} \Rightarrow {\rm{E}} = 14\;V\)
19.4
Đề bài:
Mắc hai đầu một biến trở R vào hai cực của một nguồn điện không đổi. Điều chỉnh giá trị biến trở R. Bỏ qua điện trở của các dây nối. Đồ thị biểu diễn sự phụ thuộc của hiệu suât nguồn điện vào R như Hình 19.2.
a) Xác định điện trở trong của nguồn điện.
b) Tìm giá trị R của biến trở để hiệu suất nguồn điện bằng 70%.
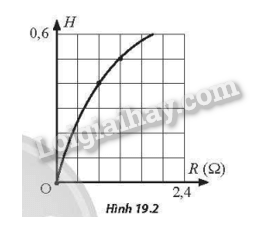
Phương pháp giải
Áp dụng công thức \(H = \frac{U}{{\rm{E}}} = \frac{R}{{R + r}}\)

a) Từ \(H = \frac{U}{{\rm{E}}} = \frac{R}{{R + r}}\)
Sử dụng các điểm trên đường đồ thị (0,8;0,4) hoặc (1,2;0,5).Suy ra: r=1,2Ω
b) Thay H = 0,7 ; ta tính được: R=2,8Ω
19.5
Đề bài:
Một biến trở được mắc vào hai cực của một nguồn điện không đổi có điện trở trong 2,0Ω. Khi thay đổi giá trị biến trở, ta thu được đồ thị biểu diễn sự phụ thuộc của công suất toả nhiệt trên biến trở vào cường độ dòng điện chạy trong mạch như Hình 19.3. Bỏ qua điện trở của các dây nối. Giá trị biến trở tương ứng với điểm M trên đồ thị bằng bao nhiêu?
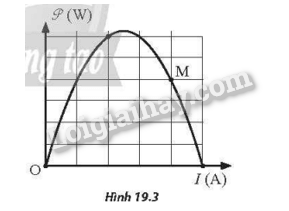
Phương pháp giải
Quan sát và phân tích đồ thị

a có biểu thức P theo I: P=UI=(E−rI)I=−rI2+EI . Đường biểu diễn P theo I là một parabol như Hình 19.3.
Mặt khác, từ các bài tập trước, ta có kết quả: Khi chỉnh R = r thì công suất tiêu thụ trên R đạt cực đại. Suy ra, dòng điện ứng với trường hợp này: \({I_{{\rm{P}}\max }} = \frac{{\rm{E}}}{{R + r}} = \frac{{\rm{E}}}{{2r}}\). Mặt khác, dòng điện ứng với điểm M: \({I_M} = \frac{{\rm{E}}}{{{R_M} + r}}\). Từ đồ thị, ta thấy: IM=4 ô; IPmax=2,5 ô. Nên: \(\frac{{{I_M}}}{{{I_{{\rm{P}}\max }}}} = \frac{{\rm{E}}}{{\left( {{R_M} + r} \right)}} \cdot \frac{{2r}}{{\rm{E}}} = \frac{{2r}}{{{R_M} + r}} = \frac{4}{{2,5}} \Rightarrow {R_M} = 0,5\Omega \)
19.6
Đề bài:
Mắc hai đầu một biến trở R vào hai cực của một nguồn điện không đổi. Điều chỉnh giá trị biến trở R. Bỏ qua điện trở của các dây nối. Đồ thị biểu diễn sự phụ thuộc của công suất toả nhiệt trên biến trở P theo R như Hình 19.4.
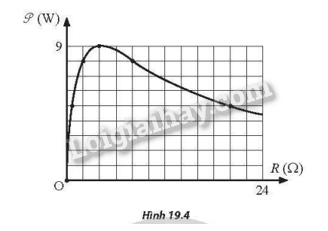
a) Tính suất điện động và điện trở trong của nguồn điện.
b) Giả sử tăng R tuyến tính theo thời gian, bắt đầu từ giá trị 0 đến rất lớn. Thời điểm t=12,5 s kể từ lúc bắt đầu tăng, công suất P đạt giá trị cực đại. Tính khoảng thời gian giữa hai lần liên tiếp công suất P đạt giá trị 5 W.
Phương pháp giải
Quan sát và phân tích đồ thị\(R + \frac{{{r^2}}}{R} \ge 2r\)

a) Ta có, công suất toả nhiệt trên biến trở: \({\rm{P}} = R{I^2} = R\frac{{{{\rm{E}}^2}}}{{{{\left( {R + r} \right)}^2}}} = \frac{{{{\rm{E}}^2}}}{{R + 2r + \frac{{{r^2}}}{R}}}\)
Áp dụng bất đẳng thức Cauchy ta có: \(R + \frac{{{r^2}}}{R} \ge 2r\) Dấu "=” của biểu thức này ( R = r) tương ứng với giá trị cực đại của P: \({{\rm{P}}_{{\rm{max}}}} = \frac{{{{\rm{E}}^2}}}{{4r}}\)
Từ đồ thị, ta có: r=4Ωvà Pmax=9 W .
Thay vào: \({{\rm{P}}_{\max }} = \frac{{{{\rm{E}}^2}}}{{4r}} \Rightarrow 9 = \frac{{{{\rm{E}}^2}}}{{4.4}} \Rightarrow {\rm{E}} = 12\;V\)
b) Với P=5 W ta thấy trên đồ thị có một giá trị tương ứng là R2=20Ω. Giá trị R1 còn lại thoả điều kiện R1R2=r2⇒R1⋅20=42⇒R1=0,8Ω
Từ đề bài, ta có: R=0,32t(Ω), (t tính bằng s). Từ đó, thời gian cần tìm là:
\({\rm{\Delta }}t = \frac{{20 - 0,8}}{{0,32}} = 60{\rm{\;s}}\)
19.7
Đề bài:
Xét mạch điện như Hình 19.5. Bỏ qua điện trở của các dây nối và của ampe kế A. Biết R1=4Ω;R2=2Ω;R3=8Ω;R4=6Ω. Ampe kế chỉ 0,4 A và hiệu suất của nguồn bằng 80%.
a) Tính suất điện động P và điện trở trong r.
b) Tính nhiệt lượng toả ra trên điện trở R4 sau 25 s.
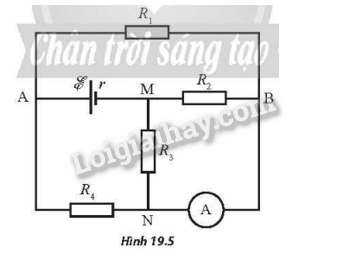
Phương pháp giải
Phân tích lại mạch điện

a) Chập các điểm N và B (do điện trở ampe kế không đáng kể). Vẽ lại mạch như hình dưới.
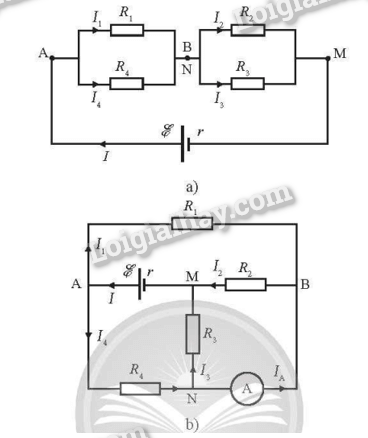
Điện trở tương đương mạch ngoài: \({R_{{\rm{AM}}}} = {R_{{\rm{AB}}}} + {R_{{\rm{BM}}}} = 2,4 + 1,6 = 4{\rm{\Omega }}\)
Hiệu suất: \(H = \frac{R}{{R + r}} \Rightarrow 0,8 = \frac{4}{{4 + r}} \Rightarrow r = 1{\rm{\Omega }}\)
Dòng điện trong mạch và các hiệu điện thế: \(\begin{array}{l}I = \frac{{\rm{E}}}{{{R_{AM}} + r}} = \frac{{\rm{E}}}{{4 + r}} \Rightarrow {U_{AB}} = \frac{{2,4{\rm{E}}}}{{4 + r}}\\ \Rightarrow {I_4} = \frac{{0,4{\rm{E}}}}{{4 + r}};{U_{BM}} = \frac{{1,6{\rm{E}}}}{{4 + r}} \Rightarrow {I_3} = \frac{{0,2{\rm{E}}}}{{4 + r}}\end{array}\)
Từ đó: \({I_A} = {I_4} - {I_3} \Rightarrow \frac{{0,2{\rm{E}}}}{{4 + 1}} = 0,4\;A \Rightarrow {\rm{E}} = 10\;V\)
b) Thay vào: \({I_4} = 0,8{\rm{\;A}} \Rightarrow {Q_4} = R{I^2}t = 6.0,{8^2}.25 = 96{\rm{\;J}}\)
