Câu hỏi/bài tập:
Giả sử một vệ tỉnh truyền thông đang đứng yên so với mặt đất ở một độ cao xác định trong mặt phẳng xích đạo Trái Đất, đường thẳng nói vệ tinh với tâm Trái Đất đi qua kinh tuyến số 0 hoặc kinh tuyến gốc. Coi Trái Đất như một quả cầu bán kính 6 400 km, khối lượng là 6.\({10^{24}}\) kg và chu kì quay quanh trục của nó là 24 h, hằng số hấp dẫn G =\(6,{67.10^{ - 11}}N.{m^2}/k{g^2}\).Sóng cực ngắn f > 30 MHz phát từ vệ tinh truyền thẳng đến các điểm nằm trên xích đạo
Trái Đất trong khoảng kinh độ nào?

Lực hấp dẫn \({F_{hd}} = \frac{{GmM}}{{{{\left( {R + h} \right)}^2}}}\)
Lực hướng tâm : \({F_{ht}} = \frac{{m{v^2}}}{{R + h}}\)
Lời giải chi tiết :
Advertisements (Quảng cáo)
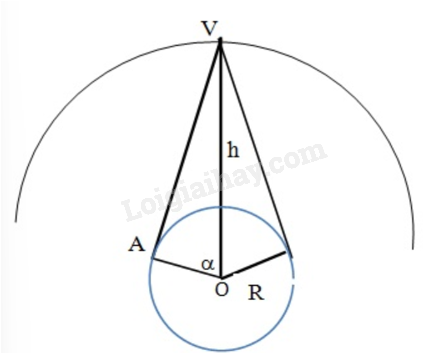
Lực hấp dẫn đóng vai trò lực hướng tâm tác dụng lên vệ tinh . Chuyển động tròn đều trên quỹ đạo bán kính R + h => \({F_{ht}} = {F_{hd}}\)
=> \(\frac{{m{v^2}}}{{R + h}} = \frac{{GmM}}{{{{\left( {R + h} \right)}^2}}}\) với \(v = \omega \left( {R + h} \right) = \frac{{2\pi (R + h)}}{T}\)
=> \(\frac{{GmM}}{{{{\left( {R + h} \right)}^2}}} = \frac{{m4{\pi ^2}(R + h)}}{{{T^2}}} = > {\left( {R + h} \right)^2} = \frac{{G{T^2}M}}{{4{\pi ^2}}}\)
=> \({(R + h)^2} = \frac{{6,{{67.10}^{ - 11}}.{{\left( {86400} \right)}^2}{{.6.10}^{24}}}}{{4{\pi ^2}}} = 7,{47.10^{22}}\left( {{m^3}} \right) = > R + h = 4,{21.10^4}km\)
\(\cos \alpha = \frac{R}{{R + h}} = \frac{{6400}}{{42100}} \approx 0,15 = > \alpha = 81,{3^0} = {81^0}{20′}\)
Sóng cực ngắn (f > 30 MHz ) phát từ vệ tinh truyền thẳng đến các điểm nằm trên xích đạo trái đất trong khoảng kinh độ từ kinh độ \({81^0}{20′}\)Đ theo hướng Tây đến kinh độ \({81^0}{20′}\)T.
