16.1
Dùng vải cọ xát một đầu thanh nhựa rồi đưa lại gần hai vật nhẹ thì thấy thanh nhựa hút cả hai vật này. Hai vật này không thể là
A. hai vật không nhiễm điện.
B. hai vật nhiễm điện cùng loại.
C. hai vật nhiễm điện khác loại.
D. một vật nhiễm điện, một vật không nhiễm điện.

Tính chất của lực tương tác giữa hai điện trường
Lời giải chi tiết :
Thanh nhựa hút cả hai vật này nên hai vật này cùng loại điện tích
Đáp án : C
16.2
Ba điện tích điểm chỉ có thể nằm cân bằng dưới tác dụng của các lực điện khi
A. ba điện tích cùng loại nằm ở ba đỉnh của một tam giác đều.
B. ba điện tích không cùng loại nằm ở ba đỉnh của một tam giác đều.
C. ba điện tích không cùng loại nằm trên cùng một đường thẳng.
D. ba điện tích cùng loại nằm trên cùng một đường thẳng.

Tính chất của lực tương tác giữa hai điện trường
Lời giải chi tiết :
Ba điện tích nằm cân bằng thì những lực điện tác dụng lên mỗi điện tích cân bằng lẫn nhau (Tức là các lực tác dụng lên mỗi điện tích cùng phương, ngược chiều và có độ lớn bằng nhau). Điều đó có nghĩa là tất cả các lực phải có cùng một giá hay ba điện tích phải nằm trên cùng một đường thẳng, và các điện tích không thể cùng dấu.
Đáp án : C
16.3
Tăng khoảng cách giữa hai điện tích lên 2 lần thì lực tương tác giữa chúng
A. tăng lên 2 lần
B. giảm đi 2 lần.
C. tăng lên 4 lần.
D. giảm đi 4 lần.

Định luật Coulomb: Lực tương tác giữa hai điện tích điểm có phương trùng với đường thẳng nối hai điện tích điểm, có độ lớn tỉ lệ thuận với tích giá trị của hai điện tích điểm và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.
Lực tương tác : \(\)\(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Lời giải chi tiết :
Ta có lực tương tác giữa hai điện tích điểm tỉ lệ nghịch với bình phương khoảng cách giữa chúng nên khi tăng khoảng cách giữa hai điện tích lên 2 lần thì lực tương tác giữa chúng giảm đi 4 lần.
Đáp án : D
16.4
Tăng đồng thời độ lớn của hai điện tích điểm và khoảng cách giữa chúng lên gấp đôi thì lực điện tác dụng giữa chúng
A. tăng lên 2 lần
B. giảm đi 2 lần
C. giảm đi 4 lần.
D. không đổi.

Định luật Coulomb: Lực tương tác giữa hai điện tích điểm có phương trùng với đường thẳng nối hai điện tích điểm, có độ lớn tỉ lệ thuận với tích giá trị của hai điện tích điểm và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.
Lực tương tác : \(\)\(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Lời giải chi tiết :
Ta có lực tương tác \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Tăng đồng thời độ lớn của hai điện tích điểm và khoảng cách giữa chúng lên gấp đôi thì lực điện tác dụng giữa chúng : \({F’} = k\frac{{\left| {2.{q_1}2.{q_2}} \right|}}{{{{\left( {2r} \right)}^2}}} = F\)
Đáp án : D
16.5
Hai quả cầu A và B có khối lượng \({m_1}\)và \({m_2}\) được treo vào điểm O bằng hai đoạn dây cách điện OA và AB (Hình 16.1). Khi tích điện cho hai quả cầu thì lực căng T của đoạn dây OA so với trước khi tích điện sẽ
A. tăng nếu hai quả cầu tích điện cùng loại.
B. giảm nếu hai quả cầu tích điện cùng loại.
C. không đồi.
D. không đổi chỉ khi hai quả cầu tích điện khác loại.

Advertisements (Quảng cáo)
Lực căng dây \(T = \left( {{m_A} + {m_B}} \right)g\)
Lời giải chi tiết :
Ta có Lực căng dây \(T = \left( {{m_A} + {m_B}} \right)g\) không phụ thuộc vào điện tích các vật
Đáp án : C
16.6
Giải thích tại sao bụi bám chặt vào các cánh quạt máy bằng nhựa mặc dù các cánh quạt này thường xuyên quay rất nhanh.

Có hai loại điện tích khác dấu là điện tích dương và điện tích âm.
Các điện tích cùng dấu đẩy nhau, khác dấu hút nhau.
Lời giải chi tiết :
Cánh quạt quay liên tục tạo ra lực ma sát, cánh quạt lúc này sẽ ma sát với không khí gây tích điện, tạo ra lực hút mà đặc biệt đối với những vật thể nhỏ và nhẹ bay trong không khí như bụi. Vì vậy, sau 1 thời gian sử dụng bụi sẽ bị hút bám dính vào cánh quạt.
16.7
a) Hãy giải thích tại sao đưa một quả cầu Q tích điện dương lại gần đầu A của thanh kim loại AB thì đầu A của thanh kim loại bị nhiễm điện âm, đầu B bị nhiễm điện dương (Hình 16.2).
b) Nếu thay thanh kim loại bằng thanh nhựa thì hai đầu của thanh này có bị nhiễm điện Hình 16.2 không? Tại sao?

Có hai loại điện tích khác dấu là điện tích dương và điện tích âm.
Lời giải chi tiết :
a) Điện tích dương ở quả cầu Q sẽ hút các êlectron tự do trong thanh kim loại AB về phía nó. Vì vậy, ở đầu A gần quả cầu Q sẽ thừa electron nên nhiễm điện âm, còn đầu B thiếu electron nên nhiễm điện dương.
b) Nếu thay thanh kim loại bằng thanh nhựa thì hai đầu của thanh này không bị nhiễm điện vì thanh nhựa không tiếp xúc hay cọ xát thì thanh nhựa không mang điện .
16.8
a) Tính lực tĩnh điện tương tác giữa hạt nhân nguyên tử helium với electron nằm trong lớp vỏ của nguyên tử này. Biết khoảng cách từ electron đền hạt nhân của nguyên tử helium là \(2,{94.10^{ - 11}}\) m, điện tích của electron là \( - 1,{6.10^{ - 19}}\) C.
b) Nếu coi electron chuyển động tròn đều dưới tác dụng của lực hút tĩnh điện
với bán kính quỹ đạo đã cho ở trên thì tốc độ góc và tốc độ của nó bằng bao
nhiêu? Biết khối lượng của electron là \(9,{1.10^{ - 31}}\) kg.

Định luật Coulomb: Lực tương tác giữa hai điện tích điểm có phương trùng với đường thẳng nối hai điện tích điểm, có độ lớn tỉ lệ thuận với tích giá trị của hai điện tích điểm và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.
Lực tương tác : \(\)\(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Lực hướng tâm : \({F_{ht}} = \frac{{m{v^2}}}{r} = mr{\omega ^2}\)
Lời giải chi tiết :
a) Hạt nhân trong nguyên tử heli có hai proton.
Vì mỗi proton mang một điện tích p = \(1,{6.10^{ - 19}}\)= e nên hạt nhân trong nguyên tử Heli mang một điện tích là: q1 = 2e
Một electron có điện tích là: q2 =\( - 1,{6.10^{ - 19}}\)C = - e
Vậy lực hút tĩnh điện giữa hạt nhân trong nguyên tử heli với một electron ở lớp vỏ nguyên tử là: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = {9.10^9}\frac{{{{\left( {1,{{6.10}^{ - 19}}} \right)}^2}}}{{{{\left( {2,{{94.10}^{ - 11}}} \right)}^2}}} = 5,{33.10^{ - 7}}N\)
b) Do electron chuyển động tròn đều quanh hạt nhân nên lực hút tĩnh điện đóng vai trò là lực hướng tâm: \({F_d} = {F_{ht}} = 5,{33.10^{ - 7}}\)
Ta có lực hướng tâm : \({F_{ht}} = \frac{{m{v^2}}}{r} = \frac{{9,{{1.10}^{ - 31}}.{v^2}}}{{2,{{94.10}^{ - 11}}}} = 5,{33.10^{ - 7}} = > v = \sqrt {\frac{{5,{{33.10}^{ - 7}}.2,{{94.10}^{ - 11}}}}{{9,{{1.10}^{ - 31}}}}} = 4,{14.10^6}m/s\)
Và ta có \({F_{ht}} = mr{\omega ^2} = > \omega = \sqrt {\frac{{{F_d}}}{{mr}}} = \sqrt {\frac{{5,{{33.10}^{ - 7}}}}{{5,{{33.10}^{ - 7}}.2,{{94.10}^{ - 11}}}}} = 1,{41.10^{17}}rad/s\)
16.9
Hai quả cầu kim loại nhỏ có cùng kích thước, cùng khối lượng 90 g, được treo vào cùng một điểm bằng hai sợi dây mảnh cách điện có cùng chiều dài 1,5 m. Truyền cho mỗi quả cầu một điện tích \(2,{4.10^{ - 7}}\) C thì chúng đẩy nhau ra xa tới lúc cân bằng thì hai điện tích cách nhau một đoạn a. Coi góc lệch của hai sợi dây so với phương thẳng đứng là rất nhỏ. Tính độ lớn của a. Lầy g = 10\(m/{s^2}\).

Lực tương tác : \(\)\(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Các điện tích cùng dấu đẩy nhau, khác dấu hút nhau.
Lời giải chi tiết :
Gọi điện tích của quả cầu là q => điện tích của mỗi quả cầu là :\({q’} = \frac{q}{2}\)
Theo đề bài ta có \(P = {F_d} = > mg = k\frac{{{q^2}}}{{{a^2}}} = > {a^2} = \frac{{k{q^2}}}{{mg}} = > a = 0,075m = 7,5cm\)
16.10
Một hệ gồm ba điện tích điểm dương q giống nhau và một điện tích điểm Q nằm cân bằng. Biết ba điện tích q nằm ở ba đỉnh của một tam giác đều. Xác định dấu, độ lớn của điện tích (theo q) và vị trí của điện tích điểm Q.

Định luật Coulomb: Lực tương tác giữa hai điện tích điểm có phương trùng với đường thẳng nối hai điện tích điểm, có độ lớn tỉ lệ thuận với tích giá trị của hai điện tích điểm và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.
Lực tương tác : \(\)\(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Có hai loại điện tích khác dấu là điện tích dương và điện tích âm.
Các điện tích cùng dấu đẩy nhau, khác dấu hút nhau.
Lời giải chi tiết :
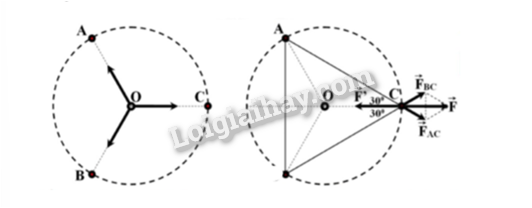
Để hệ cân bằng thì hệ lực phải đồng phẳng , Q phải mang điện tích âm , đặt tại tâm của tam giác đều và hợp lực tác dụng lên các điện tích đặt tại các đỉnh bằng 0 ( xét tại C) : \({F’} = F \Leftrightarrow k\frac{{\left| {qQ} \right|}}{{O{C^2}}} = 2k\frac{{{q^2}}}{{A{C^2}}}\cos {30^0} = > Q = - \frac{q}{{\sqrt 3 }}\)
