Câu hỏi/bài tập:
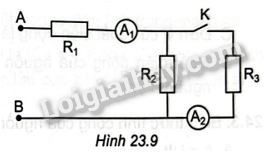
Cho mạch điện như Hình 23.9. Hiệu điện thể giữa hai đầu đoạn mạch.
AB là\({U_{AB}} = 6V\). Khi K mở ampe kế \({A_1}\) chỉ 1,2A. Khi K đóng, ampe kế \({A_1}\) và \({A_2}\) chỉ lần lượt 14A và 0,5A. Bỏ qua điện trở của các ampe kế.
Tính điện trở: \({R_1},{R_2},{R_3}\)

Vận dụng kiến thức định luật Ohm trong các đoạn mạch .
Advertisements (Quảng cáo)

Khi K mở thì \({R_1}\) nt \({R_2}\)=> \({R_1} + {R_2} = \frac{{{U_{AB}}}}{{{I_{{a_1}}}}} = \frac{6}{{1,2}} = 5\Omega \)
Khi K đóng : \({R_1}\) nt \(({R_2}//{R_3})\) => \({I_2} = {I_{{a_1}}} - {I_{{a_2}}} = 1,4 - 0,5 = 0,9A\)
Ta có : \({U_2} = {I_2}{R_2} = {U_{AB}} - {I_1}{R_1} = > 0,9{R_2} = 6 - 1,4{R_1} = > 0,9(5 - {R_1}) = 6 - 1,4{R_1}\)
=> \(4,5 - 0,9{R_1} = 6 - 1,4{R_1} = > 0,5{R_1} = 1,5 = > {R_1} = 3\Omega \)
=> \({R_2} = 5 - {R_1} = 5 - 3 = 2\Omega \)
Mà ta có : \({U_2} = {I_2}{R_2} = {U_{AB}} - {I_1}{R_1} = > 0,9{R_2} = 0,9.2 = 1,8V = > {U_3} = {U_2} = 1,8V = > {R_3} = \frac{{{U_3}}}{{{I_{{a_2}}}}} = \frac{{1,8}}{{0,5}} = 3,6\Omega \)
