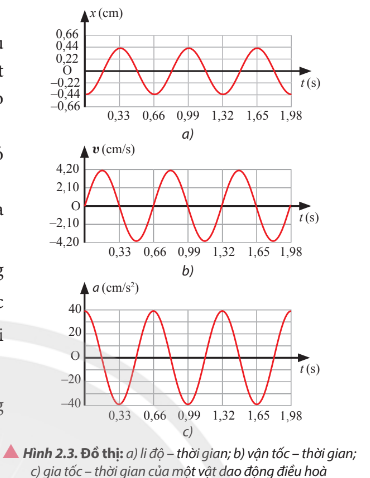
Dựa vào các đồ thị trong Hình3: a) Viết phương trình li độ, vận tốc và gia tốc của vật dao động điều hòa...

Dựa vào các đồ thị trong Hình 2.3:

a) Viết phương trình li độ, vận tốc và gia tốc của vật dao động điều hòa.

b) Mô tả định tính tính chất của li độ, vận tốc và gia tốc của vật tại các thười điểm 0,33 s; 0,495s và 0,66 s

c) Dựa vào các phương trình được xây dựng ở câu a để kiểm chứng lại mô tả định tính ở câu b

Áp dụng kiến thức đã học về phương trình dao động điều hòa: \(x = A\cos (\omega t + \varphi )\)

Biên độ dao động: A = 0,44 cm

Tốc độ cực đại: v_max = 4,2 cm/s

Gia tốc cực đại: a_max = 40 cm/s²

Chu kì của gia tốc của vật: T = 0,66 s.

Tốc độ góc: \(\omega = \frac{{2\pi }}{T} = \frac{{100}}{{33}}\pi (rad/s)\)

a) Tại thời điểm ban đầu vật đi từ biên âm tiến về VTCB nên pha ban đầu φ₀ = π(rad)

Khi đó, phương trình li độ có dạng:

x = Acos(ωt+φ₀) = 0,44cos(\(\frac{{100\pi }}{{33}}\)t+π) (cm)

Phương trình vận tốc có dạng:

v = ωAcos(ωt+φ₀+\(\frac{\pi }{2}\)) = 4,2cos(\(\frac{{100\pi }}{{33}}\)t+\(\frac{{3\pi }}{2}\)) (cm/s)

Phương trình gia tốc có dạng:

a = −ω²Acos(ωt+φ₀) = −40cos(\(\frac{{100\pi }}{{33}}\)t+π) (cm/s²)

b)

Từ đồ thị có thể thấy:

t= 0,33s: x=0,44 cm; v=0 cm/s; a=-40 cm/s²

t= 0,495s: x=0 cm; v=-4,2 cm/s; a=0 cm/s²

t= 0,66s: x=-0,44 cm; v=0 cm/s; a=40 cm/s²

c) Nghiệm lại với các phương trình.

- Tại thời điểm t = 0,5 s

x = 0,44cos(\(\frac{{100\pi }}{{33}}\).0,5+π) = −0,02 (cm)

v =4,2cos(\(\frac{{100\pi }}{{33}}\).0,5+3π2) = −4,19 (cm/s)

a =−40cos(\(\frac{{100\pi }}{{33}}\).0,5+π) = 1,9 (cm/s²)

- Tại thời điểm t = 0,75 s

x = 0,44cos(\(\frac{{100\pi }}{{33}}\).0,75+π) = −0,29 (cm)

v = 4,2cos(\(\frac{{100\pi }}{{33}}\).0,75+\(\frac{{3\pi }}{2}\)) = 3,17 (cm/s)

a = −40cos(\(\frac{{100\pi }}{{33}}\).0,75+π) = 26,2 (cm/s²)

- Tại thời điểm t = 1 s

x = 0,44cos(\(\frac{{100\pi }}{{33}}\).1+π) = 0,438 (cm)

v = 4,2cos(\(\frac{{100\pi }}{{33}}\).1+3π2) = −0,4 (cm/s)

a = −40cos(\(\frac{{100\pi }}{{33}}\).1+π) = −39,8 (cm/s²)