Câu hỏi trang 55 Khởi động
Có thể sử dụng mối liên hệ nào để xác định các đại lượng λ, v, f, T?

Dựa vào nội dung kiến thức đã học của những bài trước để trả lời.

Ta có: λ = \(\frac{v}{f}\)= vT
Bài tập luyện tập Bài 1
Một lò xo có chiều dài 1,2 m, đầu trên gắn vào một đầu thanh thép nằm ngang, đầu dưới treo một quả cân. Dao động thẳng đứng của đầu thanh thép duy trì bằng một nam châm điện để có tần số 50 Hz. Khi đó, trên lò xo có sóng dừng và trên lò xo chỉ có một nhóm vòng dao động với biên độ cực đại. Tính tốc độ truyền sóng trên lò xo.

Dựa vào nội dung kiến thức đã học về sóng để trả lời

Một nhóm vòng lò xo dao động với biên độ cực đại ⇒ n = 1
⇒L = \(\frac{\lambda }{2}\) = \(\frac{v}{{2f}}\) ⇒ v = 2Lf = 2.1,2.50 = 120 (m/s)
Bài tập luyện tập Bài 2
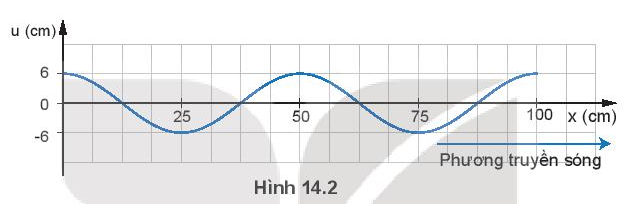
Một sóng hình sin được mô tả như Hình 14.2.
a) Xác định bước sóng của sóng.
b) Nếu chu kì của sóng là 1 s thì tần số và tốc độ truyền sóng bằng bao nhiêu?
c) Bước sóng sẽ bằng bao nhiêu nếu tần số tăng lên 5 Hz. Biết rằng tốc độ truyền sóng không đổi. Vẽ đồ thị (u - x) trong trường hợp này và đánh dấu rõ bước sóng trên đồ thị.
Advertisements (Quảng cáo)

Dựa vào nội dung kiến thức đã học về sóng để trả lời.

a) Từ đồ thị ta thấy bước sóng λ = 50(cm) = 0,5 (m)
b) Chu kì của sóng là 1 s thì f = 1 Hz
Tốc độ truyền sóng là v = λf = 0,5 (m/s)
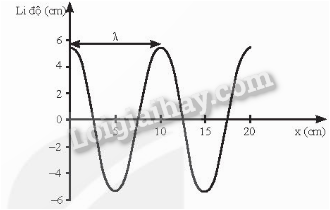
c) Tần số tăng lên 5 Hz và tốc độ truyền sóng không đổi thì bước sóng mới là
λm = \(\frac{v}{{{f_m}}}\) = 0,1(m)
Bài tập luyện tập Bài 3
Trong một thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng đơn sắc. Khoảng cách giữa hai khe là 0,6 mm. Khoảng vân trên màn quan sát đo được là 1mm. Từ vị trí ban đầu, nếu tịnh tiến màn quan sát một đoạn 25 cm lại gần mặt phẳng chứa hai khe thì khoảng vẫn mới trên màn là 0,8 mm. Tính bước sóng của ánh sáng dùng trong thí nghiệm.

Dựa vào nội dung kiến thức đã học về sóng để trả lời.

Khoảng vân tương ứng khi khoảng cách từ hai khe đến màn là D và D - 0,25m là:
\(\left\{ \begin{array}{l}{i_1} = \frac{{\lambda D}}{a} = 1\\{i_2} = \frac{{\lambda \left( {D - 0,25} \right)}}{a} = 0,8\end{array} \right. \Rightarrow \frac{D}{{D - 0,25}} = \frac{1}{{0,8}} \Rightarrow D = 1,25m\)
\( \Rightarrow \lambda = \frac{a}{D} = \frac{{0,6}}{{1,25}} = 0,48\mu m\)
