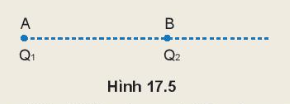
1. Đặt điện tích điểm Q1 = 6.10-8 C tại điểm A và điện tích điểm Q2 = -2.10-8 C tại điểm B cách A một khoảng bằng 3 cm (Hình 17.5). Hãy xác định những điểm mà ở đó cường độ điện trường tại đó bằng 0.
2. Cho tam giác ABC vuông tại A có AB = 3 cm và AC = 4 cm. Tại điểm B ta đặt điện tích Q1 = 4,5.10-8 C tại điểm C ta đặt điện tích Q2 = 2,1.10-8 C
a) Tính độ lớn của cường độ điện trường do mỗi điện tích trên gây ra tại A.
b) Tính cường độ điện trường tổng hợp tại A.

Dựa vào nội dung kiến thức đã học để trả lời.

1.
Cường độ điện trường bằng 0 khi:
\(\overrightarrow {{E_1}} + \overrightarrow {{E_2}} = \overrightarrow {{E_3}} = \overrightarrow 0 \Rightarrow \overrightarrow {{E_1}} = - \overrightarrow {{E_2}} \)
Advertisements (Quảng cáo)
\( \Rightarrow \left\{ \begin{array}{l}{E_1} \uparrow \downarrow {E_2}\\{E_1} = {E_2}\end{array} \right.\)
Vì |q1| > |q2| ⇒ Điểm đó thuộc đường thẳng AB và ngoài đoạn AB, gần B hơn (r1>r2)
\( \Rightarrow \left\{ \begin{array}{l}{r_1} - {r_2} = AB\\\frac{{r_1^2}}{{r_2^2}} = \frac{{\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}}\end{array} \right. \Rightarrow {r_1} = 0,071m;{r_2} = 0,041m\)
Vậy điểm cần tìm cách A 7,1 cm và cách B 4,1 cm.
2.
a) Cường độ điện trường do điện tích Q1 gây ra tại A là:
\({E_1} = \frac{{\left| {{Q_1}} \right|}}{{4\pi {\varepsilon _0}A{B^2}}} = \frac{{{{5.10}^{ - 5}}}}{{4\pi {\varepsilon _0}}}\)(V/m)
Cường độ điện trường do điện tích Q2 gây ra tại A là:
\({E_2} = \frac{{\left| {{Q_1}} \right|}}{{4\pi {\varepsilon _0}A{C^2}}} = \frac{{{{25.10}^{ - 6}}}}{{8\pi {\varepsilon _0}}}\)(V/m)
b) Ta có : \(\overrightarrow {{E_1}} \bot \overrightarrow {{E_2}} \Rightarrow E = \sqrt {E_1^2 + E_2^2} = 463427\)(V/m)
