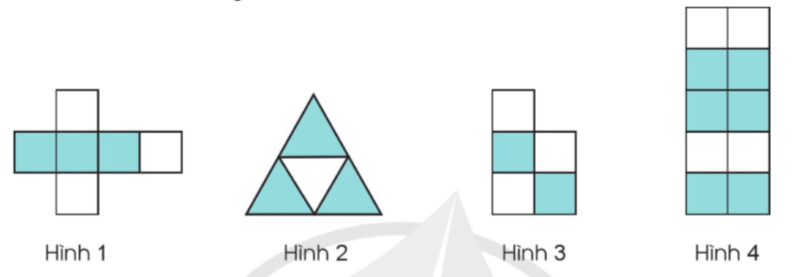
a) Đã tô màu vào $\frac{3}{5}$hình nào?
b) Phân số thứ nhất là $\frac{7}{8}$, phân số thứ hai là $\frac{3}{4}$. Hãy so sánh hai phân số đó. Tính tổng, hiệu, tích, thương của phân số thứ nhất và phân số thứ hai.

a) Phân số chỉ số phần được tô màu có tử số là số phần được tô màu, mẫu số là số phần bằng nhau.
b)
- Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới.
- Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng (hoặc trừ) hai phân số đó.
- Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số
- Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược

a) Ta thấy: Hình 4 được chia thành 10 phần bằng nhau, tô màu 6 phần.
Advertisements (Quảng cáo)
Vậy đã tô màu $\frac{6}{{10}} = \frac{3}{5}$ hình 4.
b) So sánh hai phân số $\frac{7}{8}$ và $\frac{3}{4}$
$\frac{3}{4} = \frac{{3 \times 2}}{{4 \times 2}} = \frac{6}{8}$
Vì $\frac{6}{8} < \frac{7}{8}$ nên $\frac{3}{4} < \frac{7}{8}$
Thực hiện tính:
$\frac{7}{8} + \frac{3}{4} = \frac{7}{8} + \frac{6}{8} = \frac{{13}}{8}$
$\frac{7}{8} - \frac{3}{4} = \frac{7}{8} - \frac{6}{8} = \frac{1}{8}$
$\frac{7}{8} \times \frac{3}{4} = \frac{{21}}{{32}}$
$\frac{7}{8}:\frac{3}{4} = \frac{7}{8} \times \frac{4}{3} = \frac{{28}}{{24}} = \frac{7}{6}$
