a)
b) Viết các phân số sau theo thứ tự từ lớn đến bé:

a) Muốn so sánh các phân số khác mẫu số, ta có thể quy đồng mẫu số các phân số đó, rồi so sánh các tử số của phân số mới.
b) So sánh các phân số rồi sắp xếp theo thứ tự từ lớn đến bé

a)
+) $\frac{5}{6} < \frac{7}{6}$
+) 2 = $\frac{6}{3}$
+) $\frac{3}{7}$ và $\frac{4}{{14}}$
Ta có: $\frac{3}{7} = \frac{{3 \times 2}}{{7 \times 2}} = \frac{6}{{14}}$
Vì $\frac{6}{{14}} > \frac{4}{{14}}$ nên $\frac{3}{7} > \frac{4}{{14}}$
+) $\frac{{12}}{{20}}$ và $\frac{4}{5}$
Advertisements (Quảng cáo)
Ta có: $\frac{4}{5} = \frac{{4 \times 4}}{{5 \times 4}} = \frac{{16}}{{20}}$ ; Giữ nguyên phân số: $\frac{{12}}{{20}}$
Vì $\frac{{12}}{{20}}$ < $\frac{{16}}{{20}}$ nên $\frac{{12}}{{20}}$ < $\frac{4}{5}$
Vậy ta có kết quả như sau:
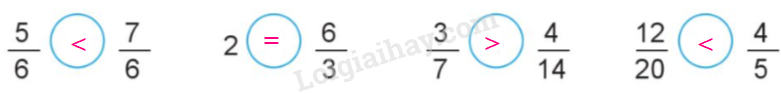
b) Quy đồng ba phân số$\frac{1}{{13}};\,\,\frac{{25}}{{13}};\,\,\frac{4}{{39}}$
$\frac{1}{{13}} = \frac{{1 \times 3}}{{13 \times 3}} = \frac{3}{{39}}$
$\frac{{25}}{{13}} = \frac{{25 \times 3}}{{13 \times 3}} = \frac{{75}}{{39}}$ ; Giữ nguyên phân số $\frac{4}{{39}}$
Vì $\frac{{75}}{{39}} > \frac{4}{{39}} > \frac{3}{{39}}$ nên $\frac{{25}}{{13}} > \frac{4}{{39}} > \frac{1}{{13}}$
Vậy các phân số đã cho xếp theo thứ tự từ lớn đến bé là $\frac{{25}}{{13}};\,\,\frac{4}{{39}};\,\,\frac{1}{{13}}$
Quy đồng ba phân số $\frac{2}{8};\,\,\frac{7}{4};\,\,\frac{9}{{16}}$
$\frac{2}{8} = \frac{{2 \times 2}}{{8 \times 2}} = \frac{4}{{16}}$
$\frac{7}{4} = \frac{{7 \times 4}}{{4 \times 4}} = \frac{{28}}{{16}}$ ; Giữ nguyên phân số $\frac{9}{{16}}$
Vì $\frac{{28}}{{16}} > \frac{9}{{16}} > \frac{4}{{16}}$ nên $\frac{7}{4} > \frac{9}{{16}} > \frac{2}{8}$
Vậy các phân số đã cho xếp theo thứ tự từ lớn đến bé là $\frac{7}{4};\,\,\frac{9}{{16}};\,\,\frac{2}{8}$
