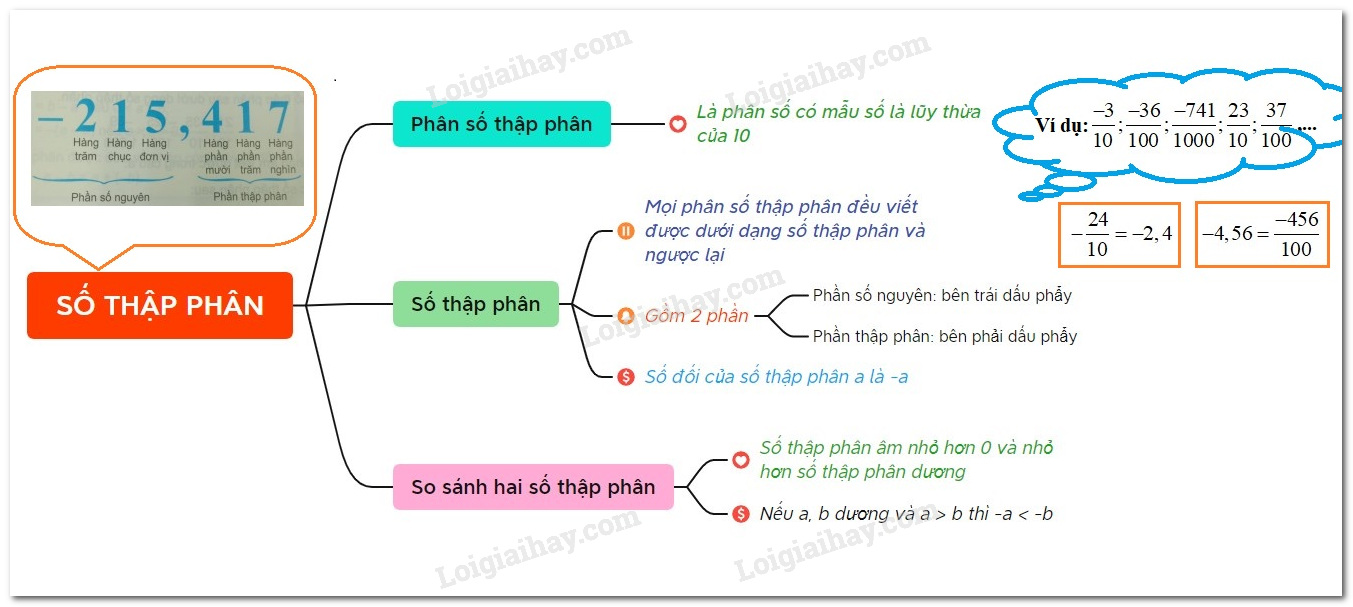
Phân số thập phân là là phân số mà mẫu là lũy thừa của $10$.
Ví dụ:
$\dfrac{7}{{10}};\dfrac{{ - 15}}{{1000}};...$ là các phân số thập phân.
- Ta viết $ - \dfrac{{15}}{{10}} = - 1,5$ và gọi $ - 1,5$ là số thập phân âm, đọc là “ âm một phẩy năm”.
- Các số $2,3;\,\,0,24;...$gọi là các số thập phân dương, đôi khi còn được viết là $ + 2,3;\,\, + 0,24;...$
- Các số thập phân dương và các số thập phân âm gọi chung là số thập phân.
Nhận xét:
- Mọi phân số thập phân đều viết được dưới dạng số thập và ngược lại.
- Số thập phân gồm hai phần:
+ Phần số nguyên viết bên trái dấu phẩy;
+ Phần thập phân viết bên phải dấu phẩy.
II. So sánh hai số thập phân
- Số thập phân âm nhỏ hơn $0$ và nhỏ hơn số thập phân dương
Advertisements (Quảng cáo)
- Nếu $a,b$ là hai số thập phân dương và $a > b$ thì $ - a < - b$.
Ví dụ:
a) $2,34 < 5,21$
b) Do $2,3 > 1,5$ nên $ - 2,3 < - 1,5$.
Chú ý:
Nếu $a < b$ và $b < c$ thì $a < c$.
III. Số đối của một số thập phân
Hai số thập phân gọi là đối nhau khi chúng biểu diễn hai phân số thập phân đối nhau.
Ví dụ:
Số đối của $ - 1,5$ là $1,5$.
Số đối của $24,3$ là $ - 24,3$