Câu hỏi/bài tập:

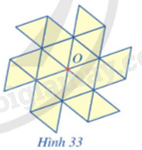
Vẽ trên giấy 18 hình tam giác đều bằng nhau và ở vị trí như Hình 33 (còn gọi là hình chong chóng).
a) Hãy đánh dấu 6 điểm mút của hình chong chóng sao cho 6 điểm mút đó là các đỉnh của một hình lục giác đều tâm O.
b) Hãy chỉ ra những phép quay tâm O giữ nguyên hình chong chóng.

a) Quan sát, đánh dấu 6 điểm có thể tạo thành một hình hình lục giác đều tâm O.
Advertisements (Quảng cáo)
b) Các phép quay thuận chiều \(a^\circ \) tâm O và các phép quay ngược chiều \(a^\circ \) tâm O, với \(a^\circ \) nhận các giá trị:
\({a_1}^\circ = \frac{{360^\circ }}{6},{a_2}^\circ = \frac{{2.360^\circ }}{6},{a_3}^\circ = \frac{{3.360^\circ }}{6},{a_4}^\circ = \frac{{4.360^\circ }}{6},{a_5}^\circ = \frac{{5.360^\circ }}{6},{a_6}^\circ = \frac{{6.360^\circ }}{6}.\)

a)
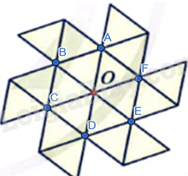
b) Các phép quay tâm O giữ nguyên hình lục giác đều:
Phép quay thuận chiều \(60^\circ ,120^\circ ,180^\circ ,240^\circ ,300^\circ ,360^\circ \) tâm O.
Phép quay ngược chiều \(60^\circ ,120^\circ ,180^\circ ,240^\circ ,300^\circ ,360^\circ \) tâm O.
