Câu hỏi/bài tập:
Một chiếc nón lá có dạng hình nón với đường kính đáy khoảng 44 cm, chiều cao khoảng 20 cm. Hỏi diện tích xung quanh của chiếc nón đó bằng bao nhiêu centimét vuông (làm tròn kết quả đến hàng đơn vị)?


Áp dụng Định lý Pytago để tính độ dài đường sinh: \(l = \sqrt {{r^2} + {h^2}} .\)
Áp dụng công thức: \({S_{xq}} = \pi rl.\)

Advertisements (Quảng cáo)
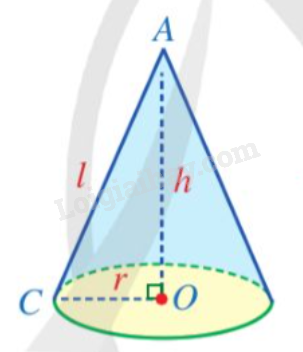
Chiếc nón lá được biểu diễn dạng hình học như hình bên.
Bán kính đáy là:
\(44:2 = 22\left( {cm} \right)\)
Đường sinh là:
\(l = \sqrt {{r^2} + {h^2}} = \sqrt {{{22}^2} + {{20}^2}} = 2\sqrt {221} \left( {cm} \right)\) (áp dụng định lý Pytago cho tam giác vuông AOC).
Diện tích xung quanh của chiếc nón là:
\({S_{xq}} = \pi rl = 3,14.22.2\sqrt {221} \approx 2054\left( {c{m^2}} \right)\)
Vậy diện tích xung quanh của chiếc nón đó là khoảng \(2054c{m^2}\).
