
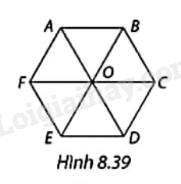
Cho lục giác đều ABCDEF như Hình 8.39.
a) Tìm ảnh của hình bình hành OABC qua phép quay thuận chiều 60o tâm O.
b) Tìm ba phép quay ngược chiều tâm O giữ nguyên lục giác đều ABCDEF.

Advertisements (Quảng cáo)
Phép quay thuận chiều \({\alpha ^o}({0^o} < {\alpha ^o} < {360^o})\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm A’ thuộc đường tròn (O;OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OA’ thì điểm A tạo nên cung AmA’ có số đo \({\alpha ^o}\)
(Định nghĩa tương tự cho phép quay ngược chiều \({\alpha ^o}\) tâm O).

Ta có AF = FE = ED = DC = CB = BA nên số đo các cung nhỏ AF, FE, ED, DC, CB, BA đều bằng \(\frac{{{{360}^o}}}{6} = {60^o}\)
a) Vậy ảnh của hình bình hành OABC qua phép quay thuận chiều 60o tâm O là hình bình hành OBCD.
b) Ba phép quay ngược chiều tâm O giữ nguyên lục giác đều ABCDEF là 60o; 120o; 180o.
