17.1
Một vật có khối lượng m đặt ở nơi có gia tốc trọng trường g. Phát biểu nào sau đây sai?
A. Trọng lực có độ lớn được xác định bởi biểu thức P = mg.
B. Điểm đặt của trọng lực là trọng tâm của vật.
C. Trọng lực tỉ lệ nghịch với khối lượng của vật.
D. Trọng lực là lực hút của Trái Đất tác dụng lên vật.

Nắm được kiến thức về trọng lực.

Trọng lực là lực hấp dẫn do Trái Đất tác dụng lên vật. Trọng lực là một trường hợp riêng của lực hấp dẫn.
Trọng lực được kí hiệu là vecto \(\overrightarrow P \), có:
+ Phương thẳng đứng;
+ Chiều hướng về phía tâm Trái Đất.
+ Điểm đặt của trọng lực gọi là trọng tâm của vật.
+ Độ lớn: P = m.g.
C sai vì theo công thức tính trọng lực thì trọng lực tỉ lệ thuận với khối lượng m của vật.
Chọn đáp án C.
17.2
Một vật đang nằm yên trên mặt đất, lực hấp dẫn do Trái Đất tác dụng vào vật có độ lớn
A. lớn hơn trọng lượng của vật.
B. nhỏ hơn trọng lượng của vật.
C. bằng trọng lượng của vật.
D. bằng 0.

Sử dụng lý thuyết về trọng lượng.

Khi vật đứng yên trên Trái Đất, trọng lượng của vật bằng độ lớn của trọng lực tác dụng lên vật: P = mg.
Chọn đáp án C.
17.3
Biết gia tốc rơi tự do ở đỉnh và ở chân một ngọn núi lần lượt là 9,809 m/s2 và 9,810 m/s2. Tỉ số trọng lượng của vật ở đỉnh núi và chân núi là
A. 0,9999. B. 1,0001. C. 9,8095. D. 0,0005.

Sử dụng công thức: P = mg.

Khi vật đứng yên trên Trái Đất, trọng lượng của vật bằng độ lớn của trọng lực tác dụng lên vật: P = mg.
Tại đỉnh núi, vật có trọng lượng: P1 = mg1.
Tại chân núi, vật có trọng lượng: P2 = mg2.
Khi đó: \(\frac{{{P_1}}}{{{P_2}}}\)=\(\frac{{m{g_1}}}{{m{g_2}}}\)=\(\frac{{{g_1}}}{{{g_2}}}\)=\(\frac{{9,809}}{{9,81}}\)≈ 0,9999.
Chọn đáp án A.
17.4
Một người đi chợ dùng lực kế đề kiểm tra khối lượng của một gói hàng. Người đó treo gói hàng vào lực kế và đọc được số chỉ của lực kế là 20 N. Biết gia tốc rơi tự do tại vị trí này là g= 10 m/s2. Khối lượng của túi hàng là
A. 2 kg. B. 20 kg. C. 30 kg. D. 10 kg.

Sử dụng công thức tính độ lớn của trọng lực: P = mg

Trọng lực tác dụng vào gói hàng có độ lớn bằng 20 N.
Mà ta có công thức tính độ lớn của trọng lực như sau:
P = mg => m = \(\frac{P}{g} = \frac{{20}}{{10}} = 2\)kg.
Vậy khối lượng của túi hàng là 2 kg.
Chọn đáp án A.
17.5
Tính trọng lượng của một nhà du hành vũ trụ có khối lượng 80 kg khi người đó ở
a) trên Trái Đất (lấy gTĐ = 9,80 m/s2).
b) trên Mặt Trăng (lấy gMT = 1,67 m/s2).
c) trên Kim tinh (lấy gKT = 8,70 m/s2).

Áp dụng công thức tính trọng lượng: P = mg.

Khi vật đứng yên, trọng lượng của vật bằng độ lớn của trọng lực tác dụng lên vật: P = mg.
a) Trọng lượng của nhà du hành vũ trụ trên Trái Đất là:
PTĐ = m.gTĐ = 80.9,8 = 784 N.
b) Trọng lượng của nhà du hành vũ trụ trên Mặt Trăng là:
PMT = m.gMT = 80.1,67 = 133,6 N.
c) Trọng lượng của nhà du hành vũ trụ trên Kim Tinh là:
PKT = m.gKT = 80.8,7 = 696 N.
17.6
Đo trọng lượng của một vật trên Trái Đất, ta được P = 19,6 N. Tính khối lượng của vật, biết gia tốc rơi tự do của vật trên mặt đất là g = 9,8 m/s2. Nếu đem vật lên Mặt Trăng có g = 1,67 m/s2 và đo trọng lượng của nó thì được bao nhiêu?

Áp dụng công thức tính trọng lượng của vật: P = mg => m = \(\frac{P}{g}\).
Khi đem vật lên mặt trăng, thế gMT vào công thức tính trọng lượng, ta được:
PMT = m.gMT

Khi vật đứng yên trên Trái Đất, trọng lượng của vật bằng độ lớn của trọng lực tác dụng lên vật.
Ta có: P1 = mg1 => m = \(\frac{{{P_1}}}{{{g_1}}}\) = \(\frac{{19,6}}{{9,8}}\) = 2 kg.
Advertisements (Quảng cáo)
Khi đem vật lên mặt trăng, ta có: PMT = m.gMT = 2.1,67 = 3,34 N.
17.7
Biết khối lượng của một hòn đá là 2 kg, gia tốc rơi tự do là 9,8 m/s2. Tính lực hút của hòn đá lên Trái Đất.

Theo định luật III Newton, lực hút của hòn đá lên Trái Đất bằng lực hút của Trái Đất lên hòn đá và bằng trọng lực: P = mg.

Theo định luật 3 Newton, lực hút của hòn đá lên Trái Đất bằng lực Trái Đất hút hòn đá và bằng trọng lượng của vật: P = mg = 19,6 N.
17.8
Một vật nặng có khối lượng 0,2 kg được treo vào một sợi dây không dãn (Hình 17.1). Xác định lực căng của dây khi cân bằng. Lấy g = 9,8 m/s2.
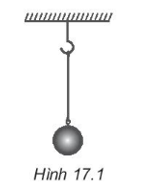

Viết phương trình cân bằng lực: \(\overrightarrow P + \overrightarrow T = \overrightarrow 0 \)=> \(\overrightarrow P = - \overrightarrow T \).

Ta có phương trình cân bằng lực: \(\overrightarrow P + \overrightarrow T = \overrightarrow 0 \)=> \(\overrightarrow P = - \overrightarrow T \)
Khi quả cầu treo dưới sợi dây cân bằng thì lực căng sợi dây bằng trọng lượng của vật: T = P = mg = 0,2.9,8 = 1,96 N.
Lực căng của dây cùng phương, ngược chiều với trọng lực và có độ lớn T = 1,96 N.
17.9
Một vật nặng có khối lượng 5 kg được treo vào các sợi dây không dãn như Hình 17.2. Xác định lực do vật nặng làm căng các sợi dây AB, AC. Lấy g = 9,8 m/s2.
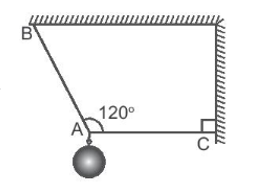

Viết phương trình cân bằng lực: \(\overrightarrow {{T_{AB}}} + \overrightarrow {{T_{AC}}} + \overrightarrow P = \overrightarrow 0 \).
Tổng hợp các lực theo quy tắc hình bình hành.
Chọn chiều dương là chiều thẳng đứng hướng xuống.
Chiếu lên chiều (+) của trục, tính độ lớn TAB, TAC theo P.
Sử dụng công thức: P = mg để tính P.

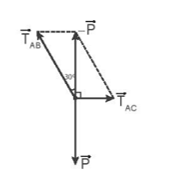
Ta có phương trình cân bằng lực: \(\overrightarrow {{T_{AB}}} + \overrightarrow {{T_{AC}}} + \overrightarrow P = \overrightarrow 0 \)⬄\(\overrightarrow {{T_{AB}}} + \overrightarrow {{T_{AC}}} = - \overrightarrow P \).
Khi vật nặng cân bằng, các lực tác dụng lên vật nặng được biểu diễn như hình vẽ. Theo hình vẽ ta có:
TAC = Ptan30o = mgtan30o = \(\frac{{49\sqrt 3 }}{3}\)N.
TAB = \(\frac{P}{{{\rm{cos3}}{{\rm{0}}^o}}}\) =\(\frac{{98\sqrt 3 }}{3}\)N.
Vậy lực do vật nặng làm căng sợi dây AC có độ lớn bằng TAC = \(\frac{{49\sqrt 3 }}{3}\)N; lực do vật nặng làm căng sợi dây AB có độ lớn bằng TAB = \(\frac{{98\sqrt 3 }}{3}\)N
17.10
Một chú khỉ diễn xiếc treo mình cân bằng trên dây thừng như Hình 17.3. Xác định lực căng xuất hiện trên các đoạn dây OA, OB. Biết chú khỉ có khối lượng 7 kg. Lấy g = 9,8 m/s2.
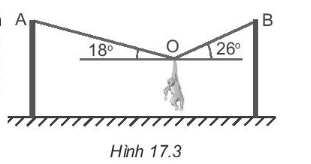

Viết phương trình cân bằng lực: \(\overrightarrow {{T_1}} + \overrightarrow {{T_2}} + \overrightarrow P = \overrightarrow 0 \).
Tổng hợp các lực theo quy tắc hình bình hành.
Chọn hệ trục Oxy có chiều dương hướng lên (Oy) và hướng từ trái sang phải (Ox).
Chiếu phương trình lần lượt lên chiều (+) của trục Oy, Ox. Giải hệ phương trình.
Sử dụng công thức: P = mg để tính P.

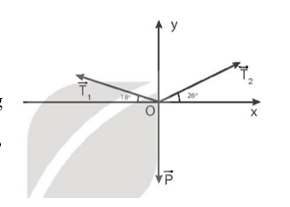
Theo công thức tính trọng lượng, ta có: P = mg = 68,6 N.
Khi vật cân bằng, ta có phương trình cân bằng lực sau: \(\overrightarrow {{T_1}} + \overrightarrow {{T_2}} + \overrightarrow P = \overrightarrow 0 \).
Chọn hệ trục Oxy có chiều dương hướng lên (Oy) và hướng từ trái sang phải (Ox).
Các lực thành phần theo trục Oy cân bằng nhau:
T1sin18o + T2sin26o – P = 0 (1)
Các lực thành phần theo trục Ox cân bằng nhau:
T1cos18o = T2cos26o (2)
Từ (1) và (2) => T1 = 88,6 N; T2 = 93,9 N.
Vậy lực căng xuất hiện trên đoạn dây OA có độ lớn T1 = 88,6 N; lực căng xuất hiện trên đoạn dây OB có độ lớn bằng T2 = 93,9 N.
17.11
Một ngọn đèn có khối lượng m = 1,2 kg được treo dưới trần nhà bằng một sợi dây. Biết dây chỉ chịu được lực căng lớn nhất là 10 N. Lấy g = 10 m/s2.
a) Chứng minh rằng không thể treo ngọn đèn này vào một đầu dây.
b) Người ta đã treo đèn này bằng cách luôn sợi dây qua một cái móc của đèn và hai đầu dây được gắn chặt trên trần nhà (Hình 17.4). Hai đầu dây có chiều dài bằng nhau và hợp với nhau một góc bằng 60°. Tính lực căng của mỗi nủa sợi dây.
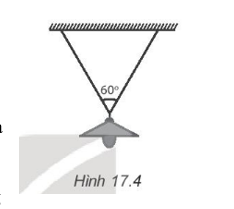

a) Tính trọng lượng cảu ngọn đền theo công thức: P = mg. So sánh P với T để kết luận.
b) Viết phương trình cân bằng lực: \(\overrightarrow {{T_1}} + \overrightarrow {{T_2}} + \overrightarrow P = \overrightarrow 0 \).
Tổng hợp các lực theo quy tắc hình bình hành.
Chọn chiều dương là chiều thẳng đứng hướng xuống.
Chiếu lên chiều (+) của trục, tính độ lớn T1 = T2 = Ttheo P.

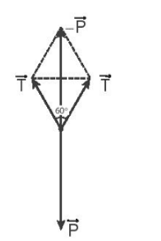
a) TA có trọng lượng của ngọn đèn: P = 12 N.
Do đó, khi treo ngọn đèn vào một đầu dây thì lực căng dây T = P = 12 N (lớn hơn 10 N), nên không thể treo ngọn đèn này vào một đầu dây.
b) Ta có phương trình cân bằng lực: \(\overrightarrow {{T_1}} + \overrightarrow {{T_2}} + \overrightarrow P = \overrightarrow 0 \) ⬄ \(\overrightarrow {{T_1}} + \overrightarrow {{T_2}} = - \overrightarrow P \)
Khi đèn cân bằng, các lực tác dụng lên đèn được biểu diễn như hình vẽ.
Chọn chiều dương là chiều thẳng đứng hướng xuống.
Chiếu lên chiều (+) của trục:
Ta có: T1 = T2 = T = \(\frac{P}{{2\cos {{30}^o}}}\)= 4\(\sqrt 3 \)N.
Vậy lực căng của mỗi sợi dây là 4\(\sqrt 3 \)N.
