Câu hỏi/bài tập:
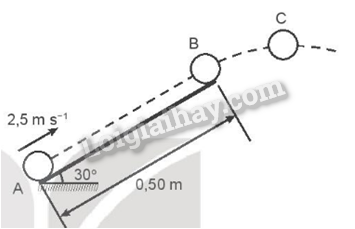
Một quả bóng khối lượng 200 g được đẩy với vận tốc ban đầu 2,5 m/s lên một mặt phẳng nghiêng, nhẵn, dài 0,5 m, hợp với phương nằm ngang góc 30° (Hình 25.1). Quả bóng chuyền động như một vật bị ném. Bỏ qua lực cản của không khí và lấy g = 9,8 m/s2. Tìm giá trị nhỏ nhất của động năng quả bóng trong quá trình nó chuyển động.
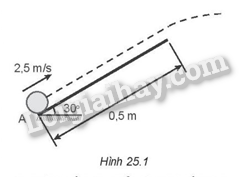

Áp dụng định luật bảo toàn cơ năng:
Vì bỏ qua mọi lực cản nên cơ năng tại A bằng cơ năng tại B: WA = WB.
Trong đó động năng được tính bằng công thức: Wđ =\(\frac{1}{2}m{v^2}\).
Và thế năng được tính bằng công thức: Wt = P.h = mgh.
Động năng cực tiểu thì bằng: Wđmin = \(\frac{1}{2}m{v_{\min }}\).

Chọn mốc thế năng là vị trí ban đầu của quả bóng trên mặt phẳng nghiêng.
Advertisements (Quảng cáo)
Đổi m = 200 g = 0,2 kg.
Vì bỏ qua mọi lực cản nên cơ năng tại A bằng cơ năng tại B: WA = WB.
=>\(\frac{1}{2}mv_A^2 = \frac{1}{2}mv_B^2 + mg{h_B}\) => \(\frac{1}{2}0,2.2,{5^2} = \frac{1}{2}.0,2.v_B^2 + 0,2.9,8.0,5.\sin {30^o}\)
=> vB ≈ 1,16 m/s.
Tại B, coi vật chuyển động bị ném nghiêng 30o so với phương ngang.
Vận tốc theo phương nằm ngang: vBx = vBcos30o.
Vận tốc theo phương này không thay đổi trong quá trình chuyển động.
Vận tốc theo phương thẳng đứng: vBy = vBsin30o.
Ở điểm cao nhất tại C thì: vC = vCx + vCy
Mà: vCy = 0 => vC = vCx = vBcos30o.
Động năng cực tiểu bằng: Wđmin = \(\frac{1}{2}m{({v_B}\cos {30^o})^2}\)≈ 0,10 J.
