Bài 26.1 trang 48, 49, 50 SBT Vật lý 10 - Kết nối tri thức: Một ô tô mô hình được thả nhẹ từ trạng thái nghỉ từ độ cao h của một cái rãnh không ma sát...

Một ô tô mô hình được thả nhẹ từ trạng thái nghỉ từ độ cao h của một cái rãnh không ma sát. Rãnh được uốn thành đường tròn có đường kính D ở phía cuối như trên Hình 26.1. Ô tô này trượt trên rãnh được cả vòng tròn mà không bị rơi. Giá trị tối thiểu của h là

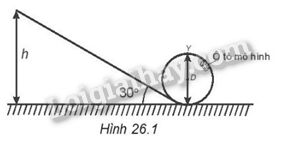
A. \(\frac{{5D}}{4}\). A. \(\frac{{3D}}{2}\). A. \(\frac{{5D}}{2}\). A. \(\frac{{5D}}{3}\).

Để ô tô này trượt trên rãnh được cả vòng tròn mà không bị rơi thì lực nén lên vòng tròn phải lớn hơn hoặc bằng 0.

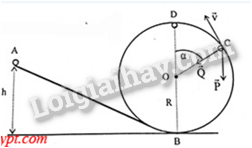
Chọn gốc thế năng tại điểm B như hình vẽ.

Áp dụng định luật bảo toàn cơ năng cho hai điểm A và C, ta có:

mgh = mgR(1 + cosα) + 0,5mv² à v² = 2gh – 2gR(1 + cosα)

Theo định luật II Newton, ta có: \(\overrightarrow Q + \overrightarrow P = m\overrightarrow a \)

Hay: Q + mgcosα = m\(\frac{{{v^2}}}{R}\)è Q = mg(\(\frac{{2h}}{R}\) - 2 – 3cosα) = N

Để ô tô có thể vượt qua hết vòng xiếc thì lực nén lên vòng tròn: N_min ≥ 0

ó mg(\(\frac{{2h}}{R}\) - 5) ≥ 0 => h ≥ 2,5R ó h ≥ \(\frac{{5D}}{4}\).

Chọn đáp án A.