Áp dụng định luật bảo toàn cơ năng. Phân tích và giải Bài 33.8 - Bài 33. Biến dạng của vật rắn trang 64, 65 - SBT Vật lý 10 Kết nối tri thức.
Câu hỏi/bài tập:
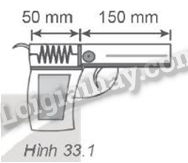
Một súng lò xo gồm lò xo chiều dài tự nhiên 200 mm, độ cứng k = 2 000 N/m và đạn có khối lượng m = 50 g. Ban đầu lò xo bị nén đến chiều dài 50 mm (Hình 33.1). Hãy tính tốc độ của viên đạn khi bắn ra khỏi nòng súng.
Áp dụng định luật bảo toàn cơ năng:
Trong đó: W = Wt + Wđ = \(\frac{1}{2}k{x^2} + \frac{1}{2}m{v^2}\).
Advertisements (Quảng cáo)
Ban đầu lò xo bị nén, thế năng đàn hồi dự trữ trong lò xo bằng W = \(\frac{1}{2}k{x^2}\).
Khi bắn, thế năng đàn hồi cuae lò xo sẽ chuyển hóa thành động năng và truyền cho viên đạn: Wđ = \(\frac{1}{2}m{v^2}\).
Áp dụng định luật bảo toàn năng lượng, ta có: \(\frac{1}{2}k{x^2}\)= \(\frac{1}{2}m{v^2}\)
=> v = x\(\sqrt {\frac{k}{m}} \)= 0,15.\(\sqrt {\frac{{2000}}{{0,05}}} \)= 30 m/s.