Câu hỏi trang 113
| Mở đầu:Trong một chiếc cầu treo như cầu Brooklyn (Brúc-klin), đường cong duyên dáng của dây cáp chính là nét căn bản để tạo nên sự hấp dẫn của nó. Những chiếc cầu này được nhìn nhận vừa như nhữ công trình nghệ thuật vừa như những kì quan kỹ thuật. Nhờ có sự biến đổi hình dạng, tức là biến dạng mà những dây cáp dẻo dai của cầu chịu được những lực rất lớn tác dụng lên cầu.
Biến dạng được phân loại như thế nào?
|

Liên hệ thực tế

Biến dạng được phân loại:
+ Biến dạng kéo
+ Biến dạng nén
Câu hỏi trang 114
Quan sát, trả lời câu hỏi và thảo luận
|
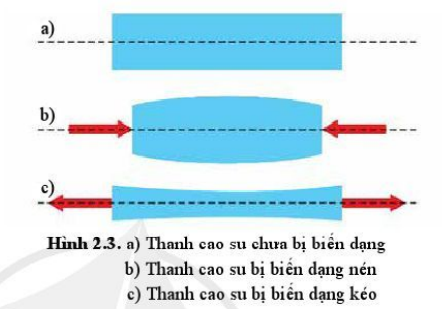
Thảo luận về kết quả (hình dạng, kích thước) của biến dạng kéo và biến dạng nén ở hình 2.3b và 2.3c.
|

Quan sát hình vẽ

Trong hình 2.3b, thanh cao su bị biến dạng nén: chiều dài bị ngắn đi, chiều rộng dài ra
Trong hình 2.3c, thanh cao su bị biến dạng kéo: chiều dài cao su dài thêm, chiều rộng ngắn lại.
Câu hỏi trang 115
Quan sát, trả lời câu hỏi và thảo luận
|
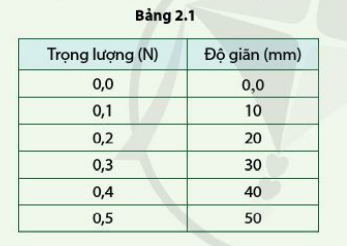
Các kết quả trong bảng 2.1 gợi cho bạn mối liên hệ gì? Hãy phát biểu mối liên hệ đó.
|

Từ bảng kết quả 2.1, ta thấy rằng trọng lượng càng tăng thì độ giãn của lò xo cũng càng tăng
=> Trọng lượng tỉ lệ thuận với độ giãn của lò xo.
Luyện tập
|
Dưới tác dụng của một lực kéo 2,5 N một lò xo dài thêm 25 mm. Độ cứng của lò xo là bao nhiêu? |

Mối liên hệ giữa lực đàn hồi, độ cứng của lò xo, độ giãn của lò xo: \(F = K.\left| {\Delta l} \right|\)
Trong đó:
+ F là lực đàn hồi của lò xo (N)
+ K là độ cứng của lò xo (N/m)
+ Δl là độ giãn của lò xo (m)

Ta có F = 2,5 N; Δl = 25 mm = 0,025 m
=> Độ cứng của lò xo là: \(K = \frac{F}{{\Delta l}} = \frac{{2,5}}{{0,025}} = 100(N/m)\)
Câu hỏi trang 116
Luyện tập
|
Bảng dưới đây là số liệu của thí nghiệm về độ giãn của lò xo:
a) Độ dài tự nhiên của lò xo là bao nhiêu? b) Hoàn thành bảng số liệu. c) Vẽ đồ thị biểu diễn mối quan hệ của trọng lượng của vật và độ giãn của lò xo. d) Đánh dấu điểm giới hạn đàn hồi trên đồ thị. e) Vùng nào trên đồ thị là vùng mà độ giãn tỉ lệ với trọng lượng? f) Trọng lượng là bao nhiêu để độ giãn lò xo là 15 mm? g) Trọng lượng là bao nhiêu để lò xo khi giãn ra có độ dài 125 mm? |

a) Chiều dài tự nhiên của lò xo là l0 = 100 mm
b) Biểu thức tính độ giãn của lò xo: \(\Delta l = l - {l_0}\)
\(\begin{array}{l}\Delta {l_0} = {l_0} - {l_0} = 0\\\Delta {l_1} = {l_1} - {l_0} = 110 - 100 = 10(mm)\\\Delta {l_2} = {l_2} - {l_0} = 120 - 100 = 20(mm)\\\Delta {l_3} = {l_3} - {l_0} = 130 - 100 = 30(mm)\\...\\\Delta {l_6} = {l_6} - {l_0} = 172 - 100 = 72(mm)\end{array}\)
|
Trọng lượng (N) |
Advertisements (Quảng cáo) 0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Chiều dài (mm) |
100 |
110 |
120 |
130 |
140 |
158 |
172 |
|
Độ giãn (mm) |
0 |
10 |
20 |
30 |
40 |
58 |
72 |
c) Đồ thị
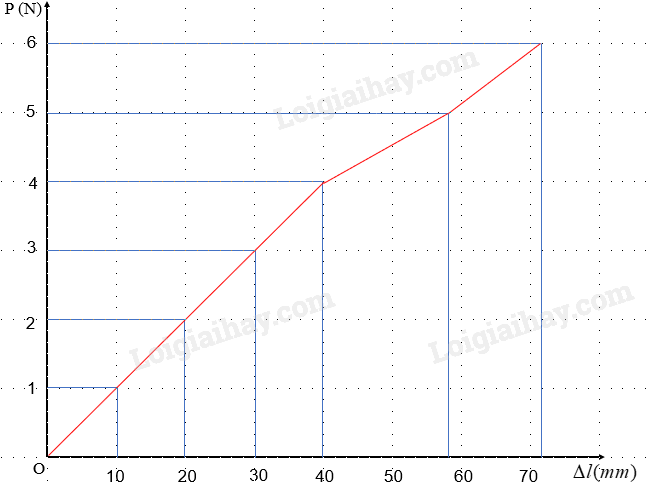
d) Đánh dấu điểm giới hạn đàn hồi trên đồ thị
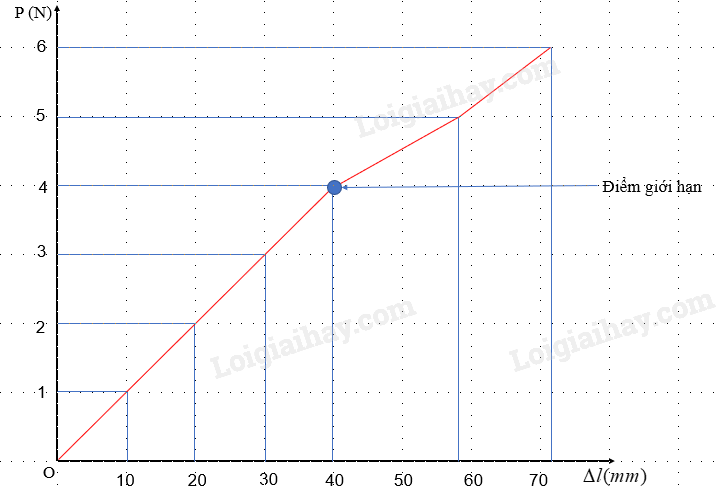
e) Vùng mà độ giãn tỉ lệ với trọng lượng
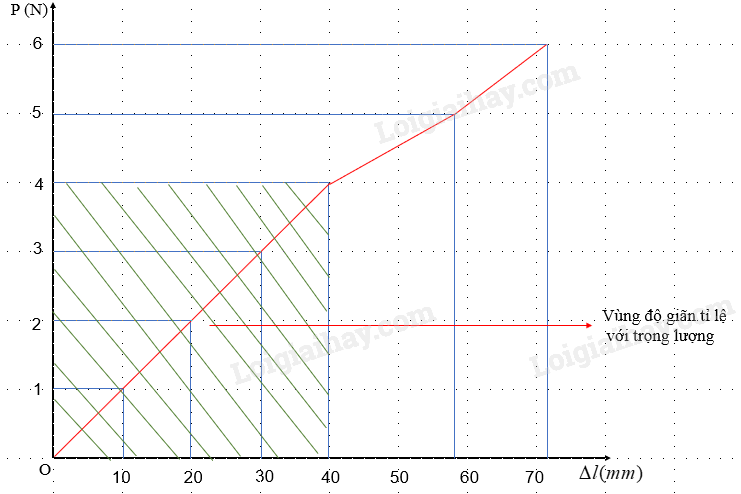
f) Ta thấy trọng lượng tăng bao nhiêu lần thì độ giãn tăng bấy nhiêu
Ta có
\(\begin{array}{l}\Delta l = 15mm = 1,5\Delta {l_1}\\ \Rightarrow P = 1,5{P_1} = 1,5.1 = 1,5(N)\end{array}\)
g) Lò xo có độ dài 125 mm
=> Lò xo giãn 125 – 100 = 25 mm
Ta có:
\(\begin{array}{l}\Delta l = 25mm = 2,5\Delta {l_1}\\ \Rightarrow P = 2,5{P_1} = 2,5.1 = 2,5(N)\end{array}\)
Câu hỏi trang 117
Vận dụng
|
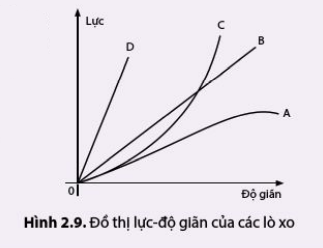
Đồ thị hình 2.9 biểu diễn mối quan hệ giữa lực tác dụng vào đầu dưới lò xo và độ giãn của nó (như thí nghiệm trên hình 2.5) với bốn lò xo A, B, C, D. a) Lò xo nào có độ cứng lớn nhất b) Lò xo nào có độ cứng nhỏ nhất? c) Lò xo nào không tuân theo định luật Hooke? |

Độ cứng của lò xo: \(K = \frac{F}{{\Delta l}}\)
Trong đồ thị, tỉ số \(\frac{F}{{\Delta l}}\) chính là hệ số góc, góc hợp bởi giữa trục hoành và đồ thị càng lớn thì hệ số góc càng lớn và ngược lại

a) Lò xo có độ cứng lớn nhất là lò xo D
b) Lò xo có độ cứng nhỏ nhất là lò xo A
c) Lò xo không tuân theo định luật Hooke là lò xo A và C.