
Cho hình lăng trụ \(ABC.A’B’C’\) có \(ABC\) là tam giác đều và \(ABB’A’\) là hình chữ nhật. Gọi M là trung điểm của BC (Hình 4).
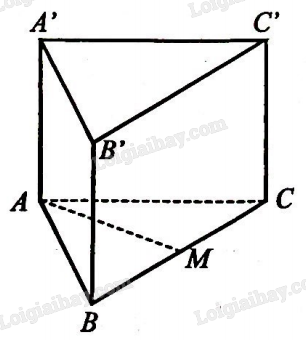
a) Số đo giữa hai đường thẳng \(AB\) và \(B’C’\) bằng:
A. \({30^0}.\)
B. \({45^0}.\)
C. \({60^0}.\)
D. \({90^0}.\)
b) Số đo giữa hai đường thẳng \(AB\) và \(CC’\) bằng:
A. \({30^0}.\)
B. \({45^0}.\)
C. \({60^0}.\)
D. \({90^0}.\)
c) Số đo giữa hai đường thẳng \(AM\) và \(A’C’\) bằng:
A. \({30^0}.\)
Advertisements (Quảng cáo)
B. \({45^0}.\)
C. \({60^0}.\)
D. \({90^0}.\)

Dựa vào các cách xác định góc giữa hai đường thẳng đã học để làm.

a) Do \(ABC\) là tam giác đều nên \(\widehat {ABC} = {60^0}.\)
Ta có: \(BC\)// \(B’C’\) nên \(\left( {AB,B’C’} \right) = \left( {AB,BC} \right) = \widehat {ABC} = {60^0}.\)
Đáp án C.
b) Do \(ABB’A’\) là hình chữ nhật nên \(\widehat {ABB’} = {90^0}.\)
Ta có: \(BB’\)// \(CC’\) nên \(\left( {AB,CC’} \right) = \left( {AB,BB’} \right) = \widehat {ABB’} = {90^0}.\)
Đáp án D.
c) Do \(ABC\) là tam giác đều nên \(\widehat {MAC} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}{.60^0} = {30^0}.\)
Ta có: \(AC\)// \(A’C’\) nên \(\left( {AM,A’C’} \right) = \left( {AM,AC} \right) = \widehat {MAC} = {30^0}.\)
Đáp án A.
