Sử dụng định lý ba đường vuông góc. Hướng dẫn giải - Bài 22 trang 95 sách bài tập toán 11 - Cánh diều - Bài 2. Đường thẳng vuông góc với mặt phẳng. Cho mặt phẳng (P) và hai điểm A, B sao cho B thuộc (P) và 4 không thuộc (P)...

Cho mặt phẳng (P) và hai điểm A, B sao cho B thuộc (P) và 4 không thuộc (P). Điểm C chuyển động trên mặt phẳng (P) thoả mãn \(\widehat {ACB} = {90^0}.\) Chứng minh rằng C chuyển động trên một đường tròn cố định trong (P).

Sử dụng định lý ba đường vuông góc.

Advertisements (Quảng cáo)
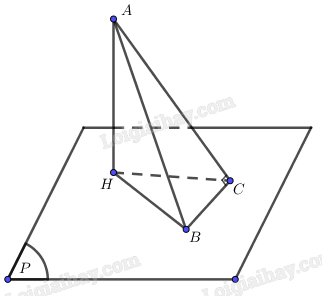
Gọi H là hình chiếu của A trên (P).
Khi đó H cố định và HC là hình chiếu của AC trên (P).
Vì \(BC \bot AC\) nên theo định lý ba đường vuông góc ta có \(BC \bot HC.\)
Do đó C chuyển động trên đường tròn đường kính HB cố định nằm trong (P).
