
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Đường thẳng \(d\) cắt \(\left( P \right)\) sao cho góc giữa đường thẳng \(d\) và mặt phẳng \(\left( P \right)\) bằng \(\varphi \) \(\left( {{0^o}
A. \({90^o} - \varphi \)
B. \({180^o} - \varphi \)
C. \(\varphi \)
D. \({90^o} + \varphi \)

Advertisements (Quảng cáo)
Gọi \({d_1}\) và \({d_2}\) lần lượt là hình chiếu của \(d\) trên mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\). Khi đó góc giữa đường thẳng \(d\) và \(\left( P \right)\) chính là góc giữa \(d\) và \({d_1}\), góc giữa đường thẳng \(d\) và \(\left( Q \right)\) chính là góc giữa \(d\) và \({d_2}\). Tính góc giữa đường thẳng \(d\) và \({d_2}\).

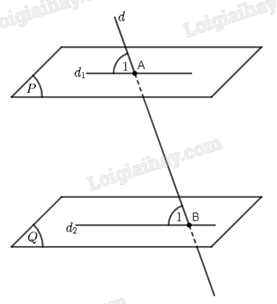
Gọi \({d_1}\) và \({d_2}\) lần lượt là hình chiếu của \(d\) trên mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\). Khi đó góc giữa đường thẳng \(d\) và \(\left( P \right)\) chính là góc giữa \(d\) và \({d_1}\), góc giữa đường thẳng \(d\) và \(\left( Q \right)\) chính là góc giữa \(d\) và \({d_2}\).
Gọi \(A\) là giao điểm của \(d\) và \({d_1}\), \(B\) là giao điểm của \(d\) và \({d_2}\). Hiển nhiên \(A \in \left( P \right)\) và \(B \in \left( Q \right)\).
Trên hình vẽ, góc giữa \(d\) và \({d_1}\) là góc \(\widehat {{A_1}}\), góc giữa \(d\) và \({d_2}\) là góc \(\widehat {{B_1}}\). Do \({d_1}\parallel {d_2}\) nên ta có \(\widehat {{A_1}} = \widehat {{B_1}}\). Suy ra góc giữa \(d\) và \(\left( Q \right)\), cũng là góc giữa \(d\) và \({d_2}\) chính là góc giữa \(d\) và \(\left( P \right)\) và bằng \(\varphi \).
Đáp án đúng là C.
