
Cho hình chóp S. ABCD có đáy ABCD là hình bình hànhvà O là giao điểm của AC và BD. Gọi M, N, P lần lượt là ba điểm nằm trên các cạnh AB, BC, SO. Xác định giao tuyến của mặt phẳng (MNP) với các mặt của hình chóp S. ABCD (nếu có).

Sử dụng kiến thức về giao tuyến giữa hai mặt phẳng để tìm giao tuyến: Đường thẳng d chung giữa hai mặt phẳng (P) và (Q) được gọi là giao tuyến của (P) và (Q), kí hiệu \(d = \left( P \right) \cap \left( Q \right)\).

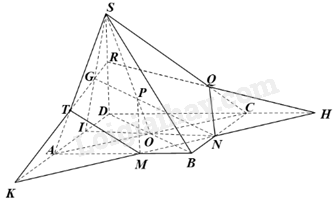
Vì \(M \in AB,N \in BC,AB \subset \left( {ABCD} \right),BC \subset \left( {ABCD} \right) \Rightarrow MN \subset \left( {ABCD} \right)\)
Advertisements (Quảng cáo)
Lại có: \(MN \subset \left( {MNP} \right) \Rightarrow \left( {MNP} \right) \cap \left( {ABCD} \right) = MN\)
Trong mặt phẳng (ABCD), gọi H là giao điểm của MN và DC, K là giao điểm của MN và AD, I là giao điểm của NO và AD.
Trong mặt phẳng (SIO), gọi G là giao điểm của NP và SI.
Trong (SAD), gọi T là giao điểm của KG và SA và R là giao điểm của KG và SD.
Trong mặt phẳng (SCD), gọi Q là giao điểm của RH và SC.
Khi đó, \(\left( {MNP} \right) \cap \left( {SAB} \right) = TM,\left( {MNP} \right) \cap \left( {SCB} \right) = NQ,\)\(\left( {MNP} \right) \cap \left( {SCD} \right) = QR,\left( {MNP} \right) \cap \left( {SAD} \right) = TR\)
