Câu hỏi/bài tập:
Bài 1.1. trang 7 SBT
Đề bài:
1.1. Khẳng định nào dưới đây là đúng khi nói về chuyển động của một vật dao động điều hòa?
A. Khi vật ở vị trí biên, vận tốc của nó cực đại.
B. Khi vật ở vị trí cân bằng, gia tốc của nó cực đại.
C. Khi vật ở vị trí biên, gia tốc của nó bằng không.
D. Khi vật ở vị trí cân bằng, tốc độ của nó cực đại.

Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Khi vật ở vị trí biên \((x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A\)
Khi vật ở vị trí cân bằng \((x = 0);v = {v_{max}} = \pm \omega A;a = 0\)

Đáp án: D. Khi vật ở vị trí cân bằng, tốc độ của nó cực đại.
Bài 1.2. trang 8 SBT
Đề bài:
1.2. Khi nói về gia tốc của vật dao động điều hòa, phát biểu nào dưới đây là đúng?
A. Gia tốc của vật dao động điều hòa luôn không đổi theo thời gian.
B. Gia tốc của vật dao động điều hòa đạt cực đại khi vật ở vị trí biên.
C. Tỉ lệ nghịch với li độ.
D. Gia tốc của vật dao động điều hòa đạt cực đại khi vật ở vị trí cân bằng.

Vận dụng kiến thức đã học về đại lượng gia tốc của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Gia tốc của vật dao động điều hòa, biến thiên theo quy luật hàm số sin (cosin) cùng chu kì T của li độ.
Mối liên hệ giữa gia tốc và li độ: \(a = - {\omega ^2}x\)
Khi vật ở vị trí biên \((x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A\)
Khi vật ở vị trí cân bằng \((x = 0);v = {v_{max}} = \pm \omega A;a = 0\)

Đáp án: B. Gia tốc của vật dao động điều hòa đạt cực đại khi vật ở vị trí biên.
Bài 1.3. trang 8 SBT
Đề bài:
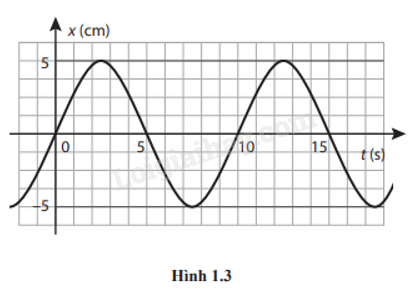
1.3. Cho đồ thị li độ - thời gian của một vật dao động điều hòa như Hình 1.3. Thông tin nào dưới đây là đúng?
A. Biên độ của dao động là 10 cm.
B. Tần số của dao động là 10 Hz.
C. Chu kì của dao động là 10 s.
D. Tần số góc của dao động là 0,1 rad/s.

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
- Đồ thị dao động điều hòa.
+ Biên độ của dao động: độ lớn cực đại của li độ theo trục 0x.
+ Chu kì của dao động: Khoảng thời gian vật thực hiện một dao động.
+ Tần số dao động: \(f = \frac{1}{T}\)Số dao động vật thực hiện được trong một giây.
+ Tần số góc của dao động: \(\omega = \frac{{2\pi }}{T} = 2\pi f\)

Biên độ của dao động là 5 cm.
Chu kì của dao động là 10 s.
Tần số của dao động là \(f = \frac{1}{T} = \frac{1}{{10}} = 0,1{\rm{ Hz}}\)
Tần số góc của dao động \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{10}} = 0,63{\rm{ rad/s}}\)
Đáp án: C. Chu kì của dao động là 10 s.
Bài 1.4. trang 8 SBT
Đề bài:
1.4. Một vật dao động điều hòa với phương trình x=4cos5t (cm) (t tính bằng s). Tốc độ của vật khi đi qua vị trí cân bằng là
A. 50 cm/s
B. 20 cm/s.
C. 100 cm/s.
D. 80 cm/s.

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với:
Khi vật ở vị trí biên \((x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A\)
Khi vật ở vị trí cân bằng \((x = 0);v = {v_{max}} = \pm \omega A;a = 0\)

Phương trình li độ của vật là: x=4cos5t.
Khi vật đi qua VTCB,
\( \Rightarrow v = {v_{max}} = \pm \omega A = \pm 5.4 = \pm 20{\rm{ cm/s}}\)
Tốc độ là độ lớn của vận tốc.
Vậy tốc độ của vật là 20 cm/s.
Đáp án: B. 20 cm/s.
Bài 1.5. trang 8 SBT
Đề bài:
1.5. Sau khi chạy một quãng đường ngắn, nhịp tim của một bạn học sinh là 96 nhịp mỗi phút. Tần số đập của tim bạn học sinh đó là:
A. 96 Hz.
B. 1,6 Hz.
C. 0,67 Hz.
D. 0,010 Hz.

Áp dụng kiến thức về tần số.
Tần số f là số dao động vật thực hiện được trong một giây.

Tần số đập của tim bạn học sinh đó là:
\(f = \frac{{9,6}}{{60}} = 1,6{\rm{ Hz}}\)
Đáp án: B. 1,6 Hz.
Bài 1.6. trang 8 SBT
Đề bài:
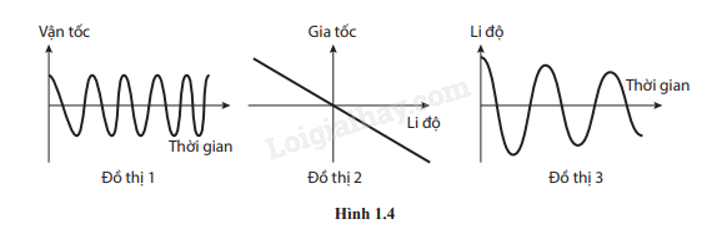
1.6. Trong ba đồ thị ở Hình 1.4, đồ thị nào mô tả vật dao động điều hòa? Gỉai thích vì sao.

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
- Đồ thị dao động điều hoà.
Advertisements (Quảng cáo)

Đồ thị 1 không mô tả vật dao động điều hòa vì dựa vào đồ thị, ta thấy chu kì giảm dần theo thời gian.
Đồ thị 2 mô tả vật dao động điều hòa vì dựa vào đồ thị, ta thấy gia tốc a tỉ lệ thuận với li độ -x.
Đồ thị 3 không mô tả vật dao động điều hòa vì dựa vào đồ thị, ta thấy biên độ thay đổi theo thời gian.
Đáp án: Đồ thị 2
Bài 1.7. trang 9 SBT
Đề bài:
1.7. Âm thoa y tế như trong Hình 1.5 được sử dụng để phát hiện triệu chứng giảm sự nhạy cảm với các rung động – một biểu hiện của chứng rối loạn thần kinh. Âm thoa này có tần số 128 Hz. Chu kì dao động của âm thoa là bao nhiêu.

Vận dụng kiến thức về tần số và chu kì của dao động điều hòa.
Tần số f là số dao động vật thực hiện được trong một giây.
Chu kì T là khoảng thời gian để vật thực hiện một dao động. \(T = \frac{1}{f}\)

Chu kì dao động của âm thoa là:
\(T = \frac{1}{f} = \frac{1}{{128}} = 7,{8125.10^{ - 3}}{\rm{ s = 7,8125 ms}}\)
Đáp án: 7,8125 ms
Bài 1.8. trang 9 SBT
Đề bài:
1.8. Một nguyên tử trong tinh thể dao động điều hòa với tần số 1,0.1014 Hz. Biên độ dao động của nguyên tử đó là 2,0.10-12 m. Xác định:
a) Tốc độ cực đại của nguyên tử.
b) Gia tốc cực đại của nguyên tử.

Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Khi vật ở vị trí biên \((x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A\)
Khi vật ở vị trí cân bằng \((x = 0);v = {v_{max}} = \pm \omega A;a = 0\)
Tốc độ là độ lớn của vận tốc.

Nguyên tử đó dao động với tần số góc:
\(\omega = 2\pi f = 2\pi {.10^{14}}{\rm{ rad/s}}\)
a) Tốc độ dao động cực đại của nguyên tử:
\({v_{max}} = \omega A = 2\pi {.10^{14}}{.2.10^{ - 12}} = 4\pi {10^{ - 12}} = 400\pi {\rm{ m/s}}\)
b) Gia tốc cực đại của nguyên tử:
\({a_{max}} = {\omega ^2}A = {\left( {2\pi {{.10}^{14}}} \right)^2}{.2.10^{ - 12}} = 8{\pi ^2}{10^{16}}{\rm{ m/}}{{\rm{s}}^2}\)
Bài 1.9. trang 9 SBT
Đề bài:
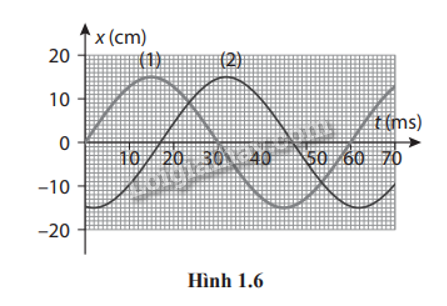
1.9. Cho hai dao động điều hòa (1) và (2) có đồ thị li độ - thời gian như Hình 1.6. Xác định:
a) Biên độ, chu kì, tẩn số của mỗi dao động.
b) Độ lệch pha của hai dao động tính theo đơn vị độ và rad.

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
- Đồ thị dao động điều hoà.
- Độ lệch pha của hai dao động cùng tần số.

a) Từ đồ thị ta thấy:
Xét dao động điều hòa (1)
- Biên độ dao động là giá trị lớn nhất của li độ: A = 15 cm
- Chu kì dao động của vật: T = 60 ms
- Tần số dao động của vật: \(f = \frac{1}{T} = \frac{1}{{{{60.10}^{ - 3}}}} = 16,7{\rm{ Hz}}\)
Xét dao động điều hòa (2)
- Biên độ dao động là giá trị lớn nhất của li độ: A = 15 cm
- Chu kì dao động của vật: T = 60 ms
- Tần số dao động của vật: \(f = \frac{1}{T} = \frac{1}{{{{60.10}^{ - 3}}}} = 16,7{\rm{ Hz}}\)
b) Hai vật dao động cùng chu kì T.
Từ đồ thị, ta thấy độ lệch thời gian của hai dao động khi cùng một trạng thái là:
\(\Delta t = 17{\rm{ ms}}\)
Độ lệch pha của hai dao động là:
\(\Delta \varphi = \frac{{\Delta t}}{T} = \frac{{17}}{{60}}\) dao động
Độ lệch pha tính theo đơn vị độ: \(\Delta \varphi = \frac{{17}}{{60}}{.360^o} = {102^o}\)
Độ lệch pha tính theo đơn vị rad: \(\Delta \varphi = \frac{{17}}{{60}}.2\pi = \frac{{17\pi }}{{30}}{\rm{ rad}}\)
Bài 1.10. trang 9 SBT
Đề bài:
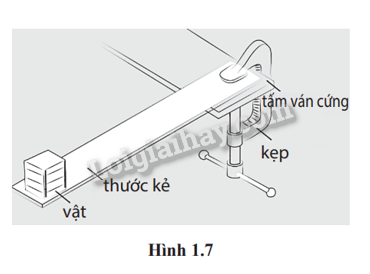
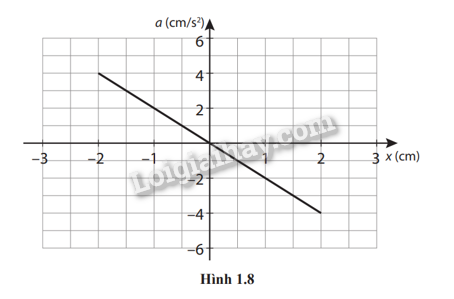
1.10. Bố trí thí nghiệm như trong Hình 1.7. Vật có khối lượng m được gắn chặt vào một đầu thước kẻ và cho dao động điều hòa tự do dưới tác dụng của cú gảy ban đầu. Một máy đo gia tốc được gắn với vật giúp ta xác định được gia tốc của nó ở các vị trí khác nhau. Đồ thị biểu diễn sự phụ thuộc của gia tốc vào li độ được cho như trong Hình 1.8.
a) Giải thích tại sao đồ thị có dạng đường thẳng với độ dốc âm.
b) Từ đồ thị xác định biên độ và gia tốc cực đại của vật.
c) Xác định tần số góc và chu kì dao động của vật.

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà.
+ Mối liên hệ giữa gia tốc và li độ: \(a = - {\omega ^2}x\)
+ Khi vật ở vị trí biên \((x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A\)
+ Khi vật ở vị trí cân bằng \((x = 0);v = {v_{max}} = \pm \omega A;a = 0\)
- Đồ thị dao động điều hòa.
+ Biên độ của dao động A: độ lớn cực đại của li độ x
+ Chu kì của dao động \(T = \frac{{2\pi }}{\omega }\)
+ Tần số góc của dao động \(\omega \)

a) Đồ thị biểu diễn mối liên hệ giữa gia tốc và li độ bằng phương trình \(a = - {\omega ^2}x\)với \(\omega \)không đổi. Nên độ dốc của đồ thị là: \( - {\omega ^2} < 0\)
Vì vậy, đồ thị có dạng đường thẳng với độ dốc âm.
b) Từ đồ thị, dễ thấy biên độ của vật là A = 2 cm, gia tốc cực đại của vật là a = 4 cm/s2.
c) Tần số góc của vật là :
\({\omega ^2} = \frac{{{a_{max}}}}{x} = \frac{4}{2} = 2{\rm{ }}\)
\( \Rightarrow \omega = \sqrt 2 {\rm{ rad/s}}\)
Chu kì dao động của vật là :
\(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\sqrt 2 }} = \pi \sqrt 2 {\rm{ s}}\)
