Câu hỏi/bài tập:
Bài 1.11. trang 10 SBT
Đề bài:
1.11. Một vật dao động điều hòa với tần số 60,0 Hz và biên độ 2,50 cm. Tính tốc độ của vật khi nó ở li độ 0,800 cm.

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với:
+ x là li độ dao động.
+ A là biên độ dao động.
+ Tần số góc của dao động là \(\omega = 2\pi f\)
+ \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t.
+ \(\varphi \) là pha ban đầu.
- Phương trình vận tốc của vật: \(v = \omega A\sin \left( {\omega t + \varphi } \right)\)
- Phương trình vuông pha giữa li độ và vận tốc: \(\frac{{{x^2}}}{{{A^2}}} + \frac{{{v^2}}}{{{\omega ^2}{A^2}}} = 1\)
Lời giải chi tiết:
Tần số góc của vật là : \(\omega = 2\pi f = 2\pi .60 = 120\pi {\rm{ rad/s}}\)
Phương trình vuông pha giữa li độ và vận tốc: \(\frac{{{x^2}}}{{{A^2}}} + \frac{{{v^2}}}{{{\omega ^2}{A^2}}} = 1\)
Thay x = 0,8 cm.
\( \Rightarrow \frac{{0,{8^2}}}{{2,{5^2}}} + \frac{{{v^2}}}{{{{\left( {120\pi .2,5} \right)}^2}}} = 1\)
\( \Rightarrow v = \pm 120\pi .2,5\sqrt {1 - \frac{{0,{8^2}}}{{2,{5^2}}}} = \pm 892,92{\rm{ cm/s}}\)
Mà tốc độ là độ lớn của vận tốc.
Vậy tốc độ của vật khi nó ở li độ 0,800 cm là 892,92 cm/s
Bài 1.12. trang 10 SBT
Đề bài:
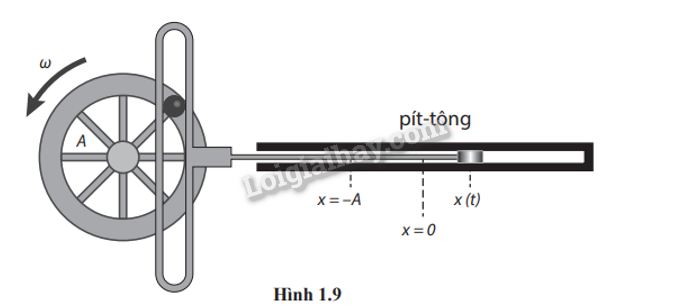
1.12. Bánh xe trong mô hình động cơ đơn giản ở Hình 1.9 có bán kính A = 0,250 m. Khi pít-tông dao động điều hòa theo phương ngang với biên độ bằng A và tần số góc \(\omega \) = 12,0 rad/s thì bánh xe quay đều liên tục với tốc độ góc \(\omega \). Tại thời điểm t = 0, pít-tông đang ở vị trí x = A.
a) Viết các phương trình li độ, vận tốc và gia tốc của pít-tông.
b) Xác định vị trí, vận tốc và gia tốc của pít-tông tại thời điểm t = 1,15 s.
c) Tính quãng đường pít-tông di chuyển được trong thời gian bánh xe quay 120 vòng.

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà.
+ Phương trình li độ: \(x = A\cos \left( {\omega t + \varphi } \right)\)
+ Phương trình vận tốc: \(v = \omega A\sin \left( {\omega t + \varphi } \right)\)
+ Phương trình gia tốc: \(a = - {\omega ^2}A\cos \left( {\omega t + \varphi } \right)\)
+ A là biên độ dao động.
+ \(\omega \)là tần số góc của dao động.
+ \(\left( {\omega t + \varphi } \right)\)là pha của dao động ở thời điểm t.
+ \(\varphi \)là pha ban đầu.
- Quãng đường vật đi hết một chu kì là S = 4A.

a) Pít-tông
Phương trình li độ của pít-tông có dạng : \(x = A\cos \left( {\omega t + \varphi } \right)\)
Phương trình vận tốc của pít-tông có dạng : \(v = \omega A\sin \left( {\omega t + \varphi } \right)\)
Phương trình gia tốc của pít-tông có dạng : \(a = - {\omega ^2}A\cos \left( {\omega t + \varphi } \right)\)
Khi t = 0, pít-tông đang ở vị trí A => pha ban đầu \(\varphi = 0\)
Từ đề bài, biên độ A = 0,25 m, tần số góc \(\omega = {\rm{12 rad/s}}\)
=> Phương trình li độ: \(x = 0,25\cos 12t{\rm{ }}\left( m \right)\)
=> Phương trình vận tốc: \(v = 3\sin 12t{\rm{ }}\left( {{\rm{m/s}}} \right)\)
=> Phương trình gia tốc: \(a = - 36\cos 12t{\rm{ }}\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\)
b) Thời điểm t = 1,15 s.
Pít-tông ở:
- Vị trí: \(x = 0,25\cos \left( {12.1,15} \right){\rm{ = 0,0827 m = 2,27 cm}}\)
- Vận tốc: \(v = 3\sin \left( {12.1,15} \right){\rm{ = 2,83 m/s}}\)
- Gia tốc: \(x = - 36\cos \left( {12.1,15} \right){\rm{ = }} - {\rm{11,91 m/}}{{\rm{s}}^2}\)
c) Khi bánh xe quay 120 vòng, pít-tông thực hiện được 120 chu kì dao động. Trong mỗi chu kì, pít-tông di chuyển quãng đường bằng 4A. Do đó, quãng đường pít-tông di chuyển trong 120 chu kì là:
s = 120.4A = 120 m.
Bài 1.13. trang 10 SBT
Đề bài:
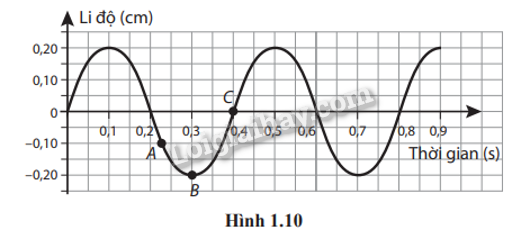
1.13. Cho đồ thị li độ - thời gian của một vật dao động điều hòa như Hình 1.10. Xác định:
a) Biên độ, chu kì, tần số và tần số góc của dao động.
b) Vận tốc và gia tốc của vật tại các điểm A, B, C.

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
+ Mối liên hệ giữa gia tốc và li độ: \(a = - {\omega ^2}x\)
+ Tính chất vuông pha giữa các đại lượng: \(v = \pm \omega \sqrt {{A^2} - {x^2}} \)
+ Khi vật ở vị trí biên \((x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A\)
+ Khi vật ở vị trí cân bằng \((x = 0);v = {v_{max}} = \pm \omega A;a = 0\)
+ A là biên độ dao động.
+ \(\omega \)là tần số góc của dao động.
+ \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t.
+ \(\varphi \)là pha ban đầu.
- Đồ thị dao động điều hoà.

a) Từ hình vẽ, vật dao động có:
Biên độ A = 0,2 cm;
Chu kì T = 0,4 s;
Tần số \(T = \frac{1}{f} = \frac{1}{{0,4}} = 2,5{\rm{ Hz;}}\)
Tần số góc \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,4}} = 5\pi {\rm{ rad/s;}}\)
b) Xác định vận tốc, gia tốc của vật tại các điểm
Tại điểm A:
Li độ x = -0,1 cm
=> Gia tốc \(a = - {\omega ^2}x = - {\left( {5\pi } \right)^2}\left( { - 0,1} \right) = 24,67{\rm{ cm/}}{{\rm{s}}^2}\)
Vận tốc: \(v = \pm \omega \sqrt {{A^2} - {x^2}} = \pm 5\pi \sqrt {0,{2^2} - {{\left( { - 0,1} \right)}^2}} = \pm 2,72{\rm{ cm/s}}\)
Theo đồ thị, vật đang di chuyển theo chiều âm của trục tọa độ => v < 0
=> Vận tốc: v = -2,72 cm/s
Tại điểm B:
Li độ x = -A = -0,2 cm
=> Vận tốc v = 0
=> Gia tốc \(a = - {\omega ^2}x = - {\left( {5\pi } \right)^2}\left( { - 0,2} \right) = 249,35{\rm{ cm/}}{{\rm{s}}^2}\)
Tại điểm C:
Li độ x = 0, vật đang di chuyển theo chiều dương của trục tọa độ.
=> Vận tốc v > 0; \(v = \omega A = 5\pi .0,2 = \pi {\rm{ cm/s}}\)
=> Gia tốc a = 0.
Bài 1.14. trang 11 SBT
Advertisements (Quảng cáo)
Đề bài:
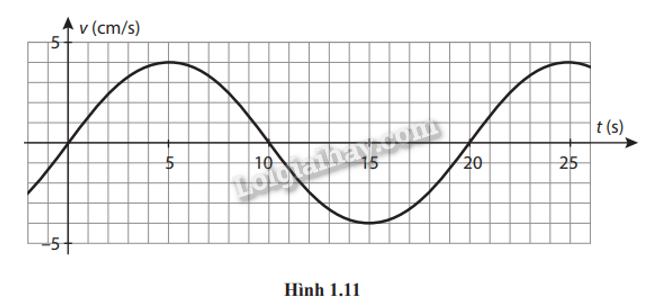
1.14. Cho đồ thị vận tốc – thời gian của một vật dao động điều hòa như Hình 1.11. Xác định:
a) Biên độ và tần số của dao động.
b) Vị trí và gia tốc của vật tại các thời điểm t = 10,0 s và t = 15,0 s.

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
+ Mối liên hệ giữa gia tốc và li độ: \(a = - {\omega ^2}x\)
+ Tính chất vuông pha giữa các đại lượng: \(v = \pm \omega \sqrt {{A^2} - {x^2}} \)
+ Khi vật ở vị trí biên \((x = \pm A);v = 0;a = {a_{max}} = \mp {\omega ^2}A\)
+ Khi vật ở vị trí cân bằng \((x = 0);v = {v_{max}} = \pm \omega A;a = 0\)
+ A là biên độ dao động.
+ \(\omega \)là tần số góc của dao động.
+ \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t.
+ \(\varphi \)là pha ban đầu.
- Đồ thị dao động điều hoà.

a) Từ đồ thị, vật có chu kì T = 20 s, vận tốc vmax = 4 cm/s
=> Tần số góc của vật: \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{20}} = 0,1\pi {\rm{ rad/s}}\)
=> Biên độ của vật: \(A = \frac{{{v_{max}}}}{\omega } = \frac{4}{{0,1\pi }} = 12,73{\rm{ = cm}}\)
b) Tại thời điểm t = 10 s, từ đồ thị, ta có v = 0, vật chuẩn bị có vận tốc âm.
=> Vật đang ở vị trí biên dương.
=> Do đó, vật ở vị trí x = A = 12,73 cm ; gia tốc \(a = - {\omega ^2}A = - 1,25{\rm{ cm/}}{{\rm{s}}^2}\)
Tại thời điểm t = 15 s, từ đồ thị, ta có v = -4 cm/s = vmax nên vật đang ở VTCB, x = 0, a = 0.
II. MỘT SỐ DAO ĐỘNG ĐIỀU HÒA THƯỜNG GẶP
Bài 1.15. trang 11 SBT
Đề bài:
1.15. Con lắc lò xo gồm lò xo khối lượng không đáng kể, một đầu cố định và đầu kia gắn với một viên bi nhỏ. Con lắc này đang dao động điều hoà theo phương nằm ngang. Lực đàn hồi của lò xo tác dụng lên viên bi luôn hướng
A. theo chiều chuyển động của viên bi.
B. về vị trí cân bằng của viên bi.
C. ngược chiều chuyển động của viên bi.
D. về vị trí biên.

Vận dụng kiến thức đã học về chu kì dao động của con lắc lò xo: \(T = 2\pi \sqrt {\frac{m}{k}} \)

Đáp án: B. về vị trí cân bằng của viên bi.
Bài 1.16. trang 11 SBT
Đề bài:
1.16. Tại một nơi xác định, chu kì của con lắc đơn tỉ lệ thuận với
A. căn bậc hai gia tốc trọng trường.
B. gia tốc trọng trường.
C. căn bậc hai chiều dài con lắc.
D. chiều dài con lắc.

Vận dụng kiến thức đã học về chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \)

Đáp án: C. căn bậc hai chiều dài con lắc.
Bài 1.17. trang 12 SBT
Đề bài:
1.17. Một con lắc lò xo gồm vật có khối lượng m và lò xo có độ cứng k không đổi, dao động điều hoà. Nếu khối lượng m = 200 g thì chu kì dao động của con lắc là 2 s. Để chu kì con lắc là 1 s thì khối lượng m bằng
A. 200 g.
B. 100 g.
C. 50 g.
D. 800 g.

Vận dụng kiến thức đã học về chu kì dao động của con lắc lò xo: \(T = 2\pi \sqrt {\frac{m}{k}} \)

\(\begin{array}{l}\frac{{{T_1}}}{{{T_2}}} = \sqrt {\frac{{{m_1}}}{{{m_2}}}} \\ \Rightarrow {m_2} = {m_1}{\left( {\frac{{{T_1}}}{{{T_2}}}} \right)^2} = 200.\frac{{{2^2}}}{{{1^2}}} = 800{\rm{ g}}\end{array}\)
Bài 1.18. trang 12 SBT
Đề bài:
1.18. Trong thực hành, để đo gia tốc trọng trường, một học sinh dùng con lắc đơn có chiều dài dây treo 80,00 cm. Khi cho con lắc dao động điều hoà, học sinh này thấy con lắc thực hiện được 20,00 dao động trong thời gian 36,00 s. Theo kết quả thí nghiệm trên, gia tốc trọng trường tại nơi học sinh làm thí nghiệm bằng
A. 9,847 cm/s2.
B. 9,874 cm/s2.
C. 9,748 cm/s2.
D. 9,783 cm/s2.

Vận dụng kiến thức đã học về chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \)

Chu kì dao động của con lắc đơn này là:
\(T = \frac{{36}}{{20}} = 1,8{\rm{ s}}\)
Gia tốc trọng trường tại nơi con lắc đơn dao động là:
\(g = \frac{{4{\pi ^2}l}}{{{T^2}}} = \frac{{4{\pi ^2}.0,8}}{{1,{8^2}}} = 9,748{\rm{ cm/}}{{\rm{s}}^2}\)
Đáp án: C. 9,748 cm/s2.
Bài 1.19. trang 12 SBT
Đề bài:
1.19. Thú nhún lò xo (Hình 1.12) là một loại đồ chơi của các em nhỏ. So sánh chu kì dao động của thú nhún nếu hai em bé có khối lượng khác nhau m1 > m2lần lượt ngồi lên con thú nhún này.


Vận dụng kiến thức đã học về chu kì dao động của con lắc lò xo: \(T = 2\pi \sqrt {\frac{m}{k}} \)

Ta có: \(T = 2\pi \sqrt {\frac{m}{k}} \)
Theo đề bài m1 > m2
=> T1 > T2
Vì vậy, em bé có khối lượng lớn hơn ngồi lên thú nhún sẽ làm thú nhún dao động với chu kì dài hơn.
Bài 1.20. trang 12 SBT
Đề bài:
1.20. Các nhạc sĩ sử dụng máy gõ nhịp như trong Hình 1.13 để rèn luyện khả năng chơi nhạc theo một nhịp độ nhất định. Thanh gõ nhịp của máy có thể coi gần đúng là một con lắc đơn. Nếu muốn máy gõ nhịp nhanh hơn thì cần điều chỉnh đầu trượt của thanh lên cao hay xuống thấp? Giải thích vì sao.


Vận dụng kiến thức đã học về chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \)

Theo đề bài, coi gần đúng thanh gõ nhịp là con lắc đơn nên chu kì của thanh gõ nhip được tính bằng công thức: \(T = 2\pi \sqrt {\frac{l}{g}} \)
Để máy gõ nhịp nhanh hơn => T nhỏ đi => l giảm xuống => Cần điều chỉnh đầu trượt của thanh xuống thấp.
Như vậy, để mãy gõ nhịp nhanh hơn thì cần điều chỉnh đầu trượt của thanh xuống thấp.
