Câu hỏi/bài tập:
III. GIAO THOA SÓNG
Bài 2.21. trang 27 SBT
Đề bài:
Điều kiện có giao thoa sóng là gì?
A. Có hai sóng chuyển động ngược chiều giao nhau.
B. Có hai sóng cùng tần số và có độ lệch pha không đổi.
C. Có hai sóng cùng bước sóng giao nhau.
D. Có hai sóng cùng biên độ, cùng tốc độ giao nhau.
Vận dụng kiến thức đã học về giao thoa: là hiện tượng hai sóng kết hợp gặp nhau tại những điểm xác định tạo nên những điểm dao động với biên độ cực đại (hai sóng tăng cường lẫn nhau) và những điểm dao động với biên độ cực tiểu (hai sóng làm suy yếu lẫn nhau).
Đáp án: B. Có hai sóng cùng tần số và có độ lệch pha không đổi.
Bài 2.22. trang 27 SBT
Đề bài:
Trong thí nghiệm giao thoa sóng trên mặt nước, hai nguồn A, B dao động cùng pha với cùng tần số f = 13 Hz. Tại một điểm M cách các nguồn A, B lần lượt là d1 = 19 cm, d2 = 21 cm thì sóng có biên độ cực đại. Giữa M và đường trung trực của AB không có dãy cực đại khác. Tốc độ truyền sóng trên mặt nước là:
A. v = 26 m/s.
B. v = 52 m/s.
C. v = 26 cm/s.
D. v = 52 cm/s.
Vận dụng kiến thức đã học về giao thoa sóng nước:
- Giao thoa là hiện tượng hai sóng kết hợp gặp nhau tại những điểm xác định tạo nên những điểm dao động với biên độ cực đại (hai sóng tăng cường lẫn nhau) và những điểm dao động với biên độ cực tiểu (hai sóng làm suy yếu lẫn nhau). - Trong giao thoa sóng nước, các điểm dao động với biên độ cực đại hay cực tiểu nằm trên các đường xác định xen kẽ trên mặt nước. Những điểm dao động với biên độ cực đại là những điểm mà hiệu đường đi của sóng từ hai nguồn đến điểm đó bằng nguyên lần bước sóng: \({x_2}-{\rm{ }}{x_1} = k\lambda \) - Những điểm dao động với biên độ cực tiểu:\({x_2}-{\rm{ }}{x_1} = \left( {k + \frac{1}{2}} \right)\lambda \)
- Tốc độ sóng là tốc độ lan truyền năng lượng của sóng trong không gian và được xác định theo công thức: v = fλ
Bước sóng của hai nguồn là: λ = d2 - d1 = 21 – 19 = 2 cm
Tốc độ truyền sóng trên mặt nước là: v = λf = 2.13 = 26 cm/s
Bài 2.23. trang 27 SBT
Đề bài:
Trong thí nghiệm Young về giao thoa ánh sáng, hai khe cách nhau a = 0,5 mm và được chiếu sáng bằng ánh sáng đơn sắc có bước sóng λ. Khoảng cách từ hai khe đến màn quan sát là 2 m. Trên màn quan sát, trong vùng giữa hai điểm M và N mà MN = 2 cm, người ta thấy tại M và N đều là vân sáng và đếm được có 10 vân tối. Bước sóng λ của ánh sáng dùng trong thí nghiệm này là:
A. 0,4 μm.
B. 0,5 μm.
C. 0,6 μm.
D.0,7 μm.
Vận dụng kiến thức đã học về thí nghiệm về giao thoa ánh sáng với hai khe sáng hẹp của Young, các vân sáng, vân tối nằm xen kẽ và cách đều nhau trên màn quan sát. Khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp được gọi là khoảng vân và tính bằng công thức: \(i = \frac{{\lambda D}}{a}\)
Ta có, khoảng vân \(i = \frac{{MN}}{{10}} = \frac{2}{{10}} = 0,2{\rm{ cm = 2 mm}}\)
Bước sóng λ của ánh sáng này là: \(\lambda = \frac{{ia}}{D} = \frac{{2.0,5}}{2} = 0,5{\rm{ \mu m}}\)
Bài 2.24. trang 27 SBT
Đề bài:
Trên giấy kẻ ô vuông, vẽ hai “sóng tam giác” giống như trong Hình 2.5. Xác định li độ tổng hợp tại các điểm thích hợp của sóng và vẽ đường biểu diễn sóng tổng hợp.
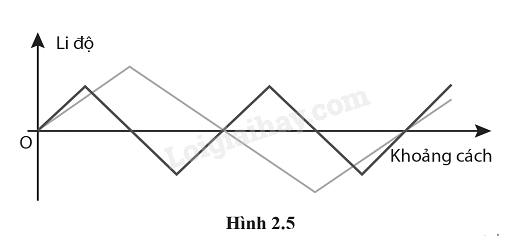
Vận dụng kiến thức đã học về đồ thị li độ – khoảng cách và các đại lượng của sóng.
- Biên độ sóng A là độ lớn cực đại của li độ của một điểm sóng.
- Chu kì sóng T: Thời gian vật thực hiện môt dao động của một điểm sóng.
- Tần số sóng: Số dao động mà mỗi điểm sóng thực hiện được trong một đơn vị thời gian: \(f = \frac{1}{T}\)
- Khi tổng hợp hai dao động, li độ của dao động chỉ bằng tổng hai li độ khi hai dao động hợp thành thực hiện theo một phương.
Xác định li độ của sóng tổng hợp là kết quả cộng đại số giá trị li độ của hai sóng thành phần tại các điểm gấp khúc của đồ thị mỗi sóng. Đường nối các điểm đó cho đường biểu diễn sóng tổng hợp của hai “sóng tam giác” như đường (3) trong hình vẽ sau.
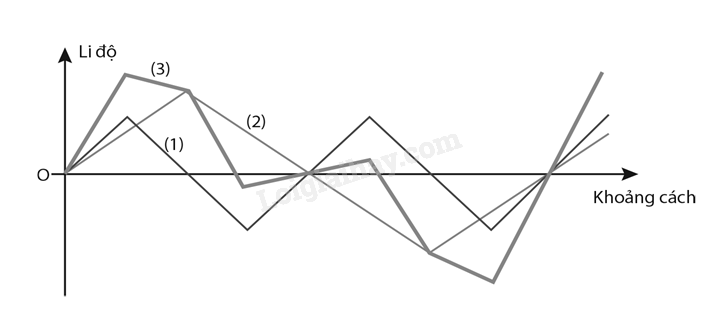
Bài 2.25. trang 28 SBT
Đề bài:
Hai sóng cùng tần số, có biên độ lần lượt là 0,20 m và 0,10 m truyền theo cùng một hướng. Vẽ phác hoạ đồ thị li độ – thời gian để minh hoạ những trường hợp sau đây: a) Hai sóng cùng pha với nhau. b) Hai sóng lệch pha nhau 90o.
Vận dụng kiến thức đã học về đồ thị li độ – khoảng cách và biên độ của hai nguồn giao thoa:
- Biên độ sóng A là độ lớn cực đại của li độ của một điểm sóng.
- Chu kì sóng T: Thời gian vật thực hiện môt dao động của một điểm sóng.
- Tần số sóng: Số dao động mà mỗi điểm sóng thực hiện được trong một đơn vị thời gian: \(f = \frac{1}{T}\)
- Biên độ dao động tổng hợp tại điểm M do hai nguồn giao thoa truyền tới với cùng phương truyền sóng: \({A_M} = 2A\left| {\cos \left( {\pi \frac{{{d_1} - {d_2}}}{\lambda } + \frac{{{\varphi _2} - {\varphi _1}}}{2}} \right)} \right|\)
+ Hai sóng cùng pha:
AMmax = 2A khi d2 – d1 = kλ \(\left( {k \in Z} \right)\)
AMmin = 0 khi \({d_2}-{\rm{ }}{d_1} = \left( {k + \frac{1}{2}} \right)\lambda {\rm{ }}\left( {k \in Z} \right)\)
Advertisements (Quảng cáo)
+ Hai sóng vuông pha:
AMmax = 2A khi \({d_2}-{\rm{ }}{d_1} = \left( {k + \frac{1}{4}} \right)\lambda {\rm{ }}\left( {k \in Z} \right)\)
AMmin = 0 khi \({d_2}-{\rm{ }}{d_1} = \left( {k + \frac{3}{4}} \right)\lambda {\rm{ }}\left( {k \in Z} \right)\)
a) Hai sóng cùng pha.
Giá trị cực đại của biên độ tổng hợp: Amax = 0,3 m Giá trị cực tiểu của biên độ tổng hợp: Amin = 0.
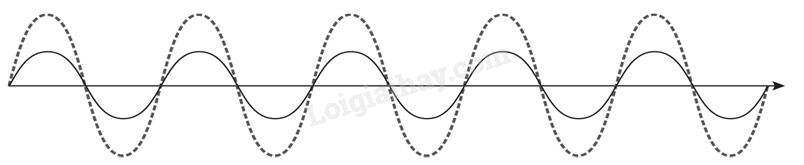b) Hai sóng lệch pha nhau 90o.
Giá trị cực đại của biên độ tổng hợp: Amax = 0,2 m Giá trị cực tiểu của biên độ tổng hợp: Amin = 0,1 m.
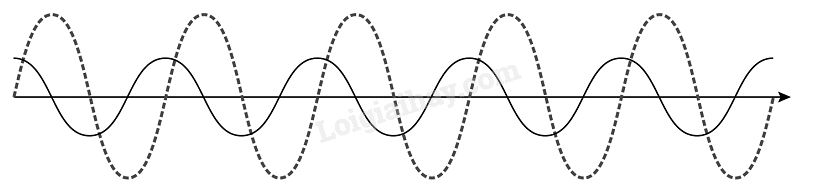
Bài 2.26. trang 28 SBT
Đề bài:
Trên mặt thoáng của chất lỏng có hai nguồn sóng A, B cách nhau 18 cm, dao động cùng pha theo phương thẳng đứng với tần số f = 10 Hz. Tốc độ truyền sóng trên mặt chất lỏng là 50 cm/s. a) Ta có thể quan sát thấy bao nhiêu điểm dao động với biên độ cực đại trên đoạn AB? b) Số điểm dao động với biên độ cực đại trên đoạn AB cũng là số vân cực đại trong vùng giao thoa sóng của hai nguồn. Xác định số vân cực tiểu trong vùng giao thoa sóng của hai nguồn trên.
Vận dụng kiến thức đã học về biên độ dao động tại điểm M của hai sóng cùng pha:
- AMmax = 2A khi d2 – d1 = kλ \(\left( {k \in Z} \right)\)
- AMmin = 0 khi \({d_2}-{\rm{ }}{d_1} = \left( {k + \frac{1}{2}} \right)\lambda {\rm{ }}\left( {k \in Z} \right)\)
- Số điểm dao động với biên độ cực đại trên đoạn L: \( - L{\rm{ }} < k\lambda < {\rm{ }}L\)
- Số điểm dao động với biên độ cực tiểu trên đoạn L: \( - L < \left( {k + \frac{1}{2}} \right)\lambda < L\)
a) Bước sóng trên mặt chất lỏng là \(\lambda = \frac{v}{f} = \frac{{50}}{{10}} = 5{\rm{ cm}}\)
Vì hai nguồn sóng A, B dao động cùng pha nên những điểm dao động với biên độ cực đại là những điểm có \({x_2}-{\rm{ }}{x_1} = k\lambda \)\(\left( {k \in Z} \right)\)
Số điểm dao động với biên độ cực đại trên đoạn AB là:
\(\begin{array}{*{20}{l}}{ - 18{\rm{ }} < k\lambda < {\rm{ }}18}\\{ \Rightarrow - 18{\rm{ }} < {\rm{ }}5k < {\rm{ }}18}\\{ \Rightarrow {\rm{ }} - 3,6{\rm{ }} < k < {\rm{ }}3,6}\\{ \Rightarrow k{\rm{ }} = \pm 3;{\rm{ }} \pm {\rm{2}};{\rm{ }} \pm {\rm{1; 0}}}\end{array}\)
Ta có thể quan sát thấy 7 điểm dao động với biên độ cực đại trên đoạn AB.
b) Vì hai nguồn sóng A, B dao động cùng pha nên những điểm dao động với biên độ cực tiểu là những điểm có \({x_2}-{\rm{ }}{x_1} = \left( {k + \frac{1}{2}} \right)\lambda \)\(\left( {k \in Z} \right)\)
Số điểm dao động cực tiểu của hai nguồn trên là:
\(\begin{array}{*{20}{l}}{ - 18{\rm{ }} < \left( {k + \frac{1}{2}} \right)\lambda < {\rm{ }}18}\\{ \Rightarrow - 18{\rm{ }} < {\rm{ 5}}\left( {k + \frac{1}{2}} \right) < {\rm{ }}18}\\\begin{array}{l} \Rightarrow {\rm{ }} - 3,6{\rm{ }} < k + \frac{1}{2} < {\rm{ }}3,6\\ \Rightarrow {\rm{ }} - 4,1{\rm{ }} < k < {\rm{ }}3,1\end{array}\\{ \Rightarrow k{\rm{ }} = - 4;{\rm{ }} \pm 3;{\rm{ }} \pm {\rm{2}};{\rm{ }} \pm {\rm{1; 0}}}\end{array}\)
Vậy hai nguồn trên có 8 điểm dao động cực tiểu.
Bài 2.27. trang 28 SBT
Đề bài:
Trong thí nghiệm giao thoa ánh sáng, hai khe Young được bố trí cách nhau a = 1,0 mm và khoảng cách từ hai khe đến màn quan sát là D = 4,8 m. Một đầu cảm biến ánh sáng được đặt tại vị trí của một vân tối trong hệ vân giao thoa. a) Khi sử dụng ánh sáng có bước sóng λ= 6,3.10–7 m thì dịch đầu cảm biến đi một đoạn ngắn nhất là bao nhiêu thì cảm biến lại nhận giá trị nhỏ nhất? b) Kết quả thu nhận của cảm biến sẽ thay đổi như thế nào nếu giữ nguyên vị trí nhưng che đi một trong hai khe sáng?
Vận dụng kiến thức đã học về thí nghiệm về giao thoa ánh sáng với hai khe sáng hẹp của Young, các vân sáng, vân tối nằm xen kẽ và cách đều nhau trên màn quan sát. Khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp được gọi là khoảng vân và tính bằng công thức: \(i = \frac{{\lambda D}}{a}\)
a) Khoảng dịch của đầu cảm biến bằng khoảng cách giữa hai vân tối gần nhất, hay chính là khoảng vân:
\(i = \frac{{\lambda D}}{a} = \frac{{0,63.4,8}}{1} = 3{\rm{ mm}}\) b) Che một trong hai khe sáng thì mỗi điểm trên màn chỉ nhận được một sóng ánh sáng nên không xảy ra hiện tượng giao thoa. Tại vị trí đầu, cảm biến sẽ nhận được cường độ sáng lớn hơn.
Bài 2.28. trang 28 SBT
Đề bài:
Ánh sáng màu vàng có bước sóng 589 nm được dùng trong thí nghiệm hai khe Young. Khoảng cách hai khe là 0,20 mm và màn đặt cách hai khe 1,20 m. a) Tính khoảng vân của hệ vân giao thoa tạo thành trên màn. b) Trên vùng quan sát vân giao thoa rộng L = 46,0 mm sẽ quan sát được bao nhiêu vân sáng, vân tối?
Vận dụng kiến thức đã học về thí nghiệm về giao thoa ánh sáng với hai khe sáng hẹp của Young, các vân sáng, vân tối nằm xen kẽ và cách đều nhau trên màn quan sát. Khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp được gọi là khoảng vân và tính bằng công thức: \(i = \frac{{\lambda D}}{a}\)
- Số vân sáng trên đoạn L: \( - L{\rm{ }} < ki < {\rm{ }}L\)
- Số vân tối trên đoạn L: \( - L < \left( {k + \frac{1}{2}} \right)i < L\)
a) Khoảng vân trên màn là :
\(i = \frac{{\lambda D}}{a} = \frac{{0,589.1,2}}{{0,2}} = 3,5{\rm{ mm}}\) b)
\(\begin{array}{l} - 23 < ki < 23\\ \Rightarrow - 23 < 3,5k < 23\\ \Leftrightarrow - 6,6 < k < 6,6\\ \Rightarrow k = 0; \pm 1; \pm 2; \pm 3; \pm 4; \pm 5; \pm 6\end{array}\)
Trên màn quan sát được 13 vân sáng.
\(\begin{array}{l} - 23 < \left( {k + \frac{1}{2}} \right)i < 23\\ \Rightarrow - 23 < 3,5\left( {k + \frac{1}{2}} \right) < 23\\ \Leftrightarrow - 6,6 - \frac{1}{2} < k < 6,6 - \frac{1}{2}\\ \Leftrightarrow - 7,1 < k < 6,1\\ \Rightarrow k = 0; - 7; \pm 1; \pm 2; \pm 3; \pm 4; \pm 5; \pm 6\end{array}\)
Trên màn quan sát được 14 vân sáng.
Bài 2.29. trang 28 SBT
Đề bài:
Một thí nghiệm giao thoa ánh sáng với hai khe Young có khoảng cách giữa hai khe 2,0 mm. Khoảng cách từ hai khe đến màn quan sát là 1,2 m. Hai khe được chiếu sáng đồng thời bởi hai ánh sáng có bước sóng λ1 = 500 nm và λ2 = 600 nm. Vân sáng chính giữa quan sát được trên màn là vị trí hai vân sáng của hai bức xạ trùng nhau. Hãy xác định khoảng cách từ vân chính giữa đến vân gần nhất cùng màu với vân chính giữa.
Vận dụng kiến thức đã học về giao thoa hai khe Young với hai ánh sáng đơn sắc khác nhau:
- Giao thoa ánh sáng với hai khe sáng hẹp của Young, các vân sáng, vân tối nằm xen kẽ và cách đều nhau trên màn quan sát. Khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp với cùng một bước sóng được gọi là khoảng vân và tính bằng công thức: \(i = \frac{{\lambda D}}{a}\)
- Tại vị trí hai vân của hai bước sóng trùng nhau: \(x = {k_1}\frac{{{\lambda _1}D}}{a} = {k_2}\frac{{{\lambda _2}D}}{a} \Rightarrow {k_1}{\lambda _1} = {k_2}{\lambda _2}{\rm{ }}\left( {{k_1},{k_2} \in Z} \right)\)
Vân chính giữa là vân sáng của hai bức xạ trùng nhau.
=> Vân cùng màu với vân chính giữa là vân sáng của hai bức xạ trùng nhau.
Chọn k1, k2 nguyên dương.
Tại vị trí đó, ta có: \(\)\(\begin{array}{l}{x_1} = {x_2}\\ \Rightarrow {k_1}\frac{{{\lambda _1}D}}{a} = {k_2}\frac{{{\lambda _2}D}}{a}\\ \Rightarrow \frac{{{k_1}}}{{{k_2}}} = \frac{{{\lambda _2}}}{{{\lambda _1}}} = \frac{{600}}{{500}} = \frac{6}{5}\end{array}\)
=> Vân gần nhất và cùng màu với vân chính giữa ứng với k1 = 6 ; k2 = 5.
\( \Rightarrow x = {k_1}\frac{{{\lambda _1}D}}{a} = 6.\frac{{0,5.1,2}}{2} = 1,8{\rm{ mm}}\)