Câu hỏi/bài tập:
IV. SÓNG DỪNG
Bài 2.30. trang 29 SBT
Đề bài:
Một sợi dây được căng theo phương thẳng đứng với hai đầu cố định. Thực hiện kích thích để trên dây có sóng dừng. Phát biểu nào dưới đây là đúng? A. Có thời điểm sợi dây duỗi thẳng. B. Hai điểm trên dây đối xứng nhau qua một nút sóng thì luôn dao động cùng pha nhau. C. Hai điểm trên dây đối xứng nhau qua một nút sóng thì luôn dao động ngược pha nhau. D. Khi giữ nguyên các điều kiện khác nhưng thả cho đầu dưới của dây tự do thì vẫn có sóng dừng ổn định trên dây.

Vận dụng kiến thức đã học về sóng dừng:
- Hiện tượng xuất hiện các điểm đứng yên ở những vị trí xác định khi đang có sóng lan truyền được gọi là hiện tượng sóng dừng. - Những điểm đứng yên gọi là nút sóng. Chính giữa hai nút sóng liên tiếp là bụng sóng.
- Khoảng cách giữa bụng sóng và nút sóng gần nhất:\(\frac{\lambda }{4}\).
- Khoảng cách giữa 2 nút hoặc 2 bụng gần nhất:\(\frac{\lambda }{2}\).

Đáp án: A. Có thời điểm sợi dây duỗi thẳng.
Bài 2.31. trang 29 SBT
Đề bài:
Một sợi dây AB đàn hồi được kéo căng và gắn cố định hai đầu. Đánh dấu điểm C chính giữa của sợi dây và hai điểm M, N đối xứng với nhau qua C. Khi trên dây quan sát được sóng dừng gồm ba nút là hai đầu A, B và điểm C thì dao động tại các điểm M và N sẽ: A. có biên độ như nhau và cùng pha. B. có biên độ khác nhau và cùng pha. C. có biên độ như nhau và ngược pha. D. có biên độ khác nhau và ngược pha.

Vận dụng kiến thức đã học về sóng dừng với hai đầu cố định: \(L = k\frac{\lambda }{2}{\rm{ }}\left( {k \in {N^*}} \right)\)
- Số bụng sóng = số bó sóng = k
- Số nút sóng = k + 1.
- Khoảng cách giữa bụng sóng và nút sóng gần nhất:\(\frac{\lambda }{4}\).
- Khoảng cách giữa 2 nút hoặc 2 bụng gần nhất:\(\frac{\lambda }{2}\).

Đáp án: C. có biên độ như nhau và ngược pha.
Bài 2.32. trang 29 SBT
Đề bài:
Để có sóng dừng trong ống cộng hưởng của âm với tần số f mà tại miệng ống tương ứng với vị trí nút sóng thì chiều dài L của ống (với k = 1, 2, 3…) là:
A. \(L = k\frac{v}{{2f}}.\)
B. \(L = k\frac{v}{f}.\)
C. \(L = \frac{v}{{kf}}.\)
D. \(L = 2\frac{v}{f}.\)

Vận dụng kiến thức đã học về sóng:
- Sóng dừng với hai đầu cố định: \(L = k\frac{\lambda }{2}{\rm{ }}\left( {k \in {N^*}} \right)\)
- Bước sóng λ là quãng đường mà sóng truyền đi trong một chu kì sóng: \(\lambda = \frac{v}{f}\)

Đáp án: A. \(L = k\frac{v}{{2f}}.\)
Bài 2.33. trang 29 SBT
Đề bài:
Khi khảo sát hiện tượng sóng dừng trên một sợi dây căng giữa hai điểm cố định, người ta thay đổi tần số dao động kích thích cho dây. Kết quả ghi nhận được hai giá trị tần số gần nhau nhất cùng cho quan sát được sóng dừng trên dây là 525 Hz và 600 Hz. Giá trị tần số nhỏ nhất có thể tạo ra sóng dừng trên dây này là :
A. 50 Hz.
B. 75 Hz.
C. 100 Hz.
D. 125 Hz.

Vận dụng kiến thức đã học về sóng:
- Sóng dừng với hai đầu cố định: \(L = k\frac{v}{{2f}}{\rm{ }}\left( {k \in {N^*}} \right)\)
- Tần số có thể tạo ra sóng dừng trên dây phù hợp điều kiện: \(\frac{{2L}}{v} = \frac{{{k_1}}}{{{f_1}}} = \frac{{{k_2}}}{{{f_2}}} = ... = \frac{{{k_n}}}{{{f_n}}}\)

\(\begin{array}{l}L = {k_1}\frac{v}{{2{f_1}}} = \left( {{k_1} + 1} \right)\frac{v}{{2{f_2}}}\\ \Rightarrow \frac{{2L}}{v} = \frac{{{k_1}}}{{{f_1}}} = \frac{{{k_1} + 1}}{{{f_2}}}\\ \Rightarrow \frac{{{k_1}}}{{525}} = \frac{{{k_1} + 1}}{{600}} \Rightarrow {k_1} = 7\\\frac{{2L}}{v} = \frac{{{k_1}}}{{{f_1}}} = \frac{7}{{525}}\\ \Rightarrow \frac{{{k_{\min }}}}{{{f_{\min }}}} = \frac{{2L}}{v} = \frac{7}{{525}} = \frac{1}{{{f_{\min }}}}\\ \Rightarrow {f_{\min }} = 75{\rm{ Hz}}\end{array}\)
Đáp án: B. 75 Hz.
Bài 2.34. trang 29 SBT
Đề bài:
Sóng dừng thiết lập trên một dây đàn hồi có các nút liên tiếp cách nhau 25,0 cm. Hãy xác định: a) Bước sóng của sóng truyền trên dây. b) Khoảng cách từ nút sóng đến bụng sóng gần nhất.

Vận dụng kiến thức đã học về sóng dừng:
- Khoảng cách giữa bụng sóng và nút sóng gần nhất:\(\frac{\lambda }{4}\).
- Khoảng cách giữa 2 nút hoặc 2 bụng gần nhất:\(\frac{\lambda }{2}\).

Advertisements (Quảng cáo)
a) Bước sóng của sóng truyền trên dây là λ = 25.2 = 50 cm b) Khoảng cách từ nút sóng đến bụng sóng gần nhất là \(\frac{\lambda }{4} = \frac{{50}}{4} = 12,5{\rm{ cm}}\)
Bài 2.35. trang 30 SBT
Đề bài:
Khi khảo sát sóng dừng của một sóng âm có tần số 2 500 Hz thì thấy giữa hai nút sóng cách nhau 21 cm thì có ba vị trí bụng sóng. a) Xác định bước sóng của sóng âm này. b) Xác định tốc độ truyền âm tại vùng không gian đang thực hiện khảo sát này.

Vận dụng kiến thức đã học về sóng dừng với hai đầu cố định: \(L = k\frac{\lambda }{2}{\rm{ }}\left( {k \in {N^*}} \right)\)
- Số bụng sóng = số bó sóng = k
- Số nút sóng = k + 1.
- Khoảng cách giữa bụng sóng và nút sóng gần nhất:\(\frac{\lambda }{4}\).
- Khoảng cách giữa 2 nút hoặc 2 bụng gần nhất:\(\frac{\lambda }{2}\).
- Tốc độ sóng là tốc độ lan truyền năng lượng của sóng trong không gian và được xác định theo công thức: v = fλ.

a) Khoảng cách giữa hai nút sóng đó là \(\frac{{3\lambda }}{2} = 21{\rm{ cm}}\)
Bước sóng của sóng âm này là \(\lambda = 21.\frac{2}{3}{\rm{ = 14 cm}}\) b) Tốc độ truyền âm tại vùng không gian đang thực hiện khảo sát này là:
v = λf = 14.10-2.2500 = 350 m/s
Bài 2.36. trang 30 SBT
Đề bài:
Một bạn học sinh dự định dùng cần rung có tần số là 20,0 Hz để tạo sóng dừng trên một sợi dây đàn hồi dài 1,2 m hai đầu cố định. Biết tốc độ truyền sóng trên dây khi quan sát được sóng dừng là 4,0 m/s. Số bụng sóng trên dây mà học sinh này có thể quan sát được là bao nhiêu?

Vận dụng kiến thức đã học về sóng dừng với hai đầu cố định: \(L = k\frac{\lambda }{2}{\rm{ }}\left( {k \in {N^*}} \right)\)
- Số bụng sóng = số bó sóng = k
- Số nút sóng = k + 1.
- Tốc độ sóng là tốc độ lan truyền năng lượng của sóng trong không gian và được xác định theo công thức: v = fλ.

Bước sóng của sóng dừng này là \(\lambda = \frac{v}{f}{\rm{ = }}\frac{4}{{20}}{\rm{ = 0,2 m}}\)
Ta có: \(L = k\frac{\lambda }{2}\)
Số bụng sóng trên dây là: \(k = \frac{{2L}}{\lambda } = \frac{{2.1,2}}{{0,2}} = 12\)
Bài 2.37. trang 30 SBT
Đề bài:
Âm do một dây đàn ghita dài 80,0 cm phát ra có tần số nhỏ nhất là bao nhiêu để có thể quan sát thấy sóng dừng trên dây? Biết tốc độ truyền sóng trên dây đàn là 4,0.102 m/s.

Vận dụng kiến thức đã học về sóng:
- Sóng dừng với hai đầu cố định: \(L = k\frac{v}{{2f}}{\rm{ }}\left( {k \in {N^*}} \right)\)
- Tần số có thể tạo ra sóng dừng trên dây phù hợp điều kiện: \(\frac{{2L}}{v} = \frac{{{k_1}}}{{{f_1}}} = \frac{{{k_2}}}{{{f_2}}} = ... = \frac{{{k_n}}}{{{f_n}}}\)

Ta có \(\lambda = \frac{v}{f}\)
Mà trong sóng dừng được cố định hai đầu: \(L = k\frac{\lambda }{2}\)
\(\begin{array}{l} \Rightarrow L = k\frac{v}{{2f}}\\ \Rightarrow f = k\frac{v}{{2L}} = k.\frac{{400}}{{2.0,8}} = 250k\end{array}\)
Tần số nhỏ nhất để quan sát sóng dừng trên dây đàn này là f = 250 Hz.
Bài 2.38. trang 30 SBT
Đề bài:
Một thí nghiệm khảo sát hiện tượng sóng dừng với sóng viba (loại sóng điện từ thường gặp ở lò vi sóng) được bố trí như Hình 2.6. Trong đó, đầu thu di chuyển từ từ trên một đường thẳng giữa máy phát sóng viba và màn phản xạ (được làm bằng kim loại) thì sẽ có những điểm thu được cường độ sóng cực đại và những điểm hầu như không ghi nhận có sóng.
a) Vẽ hình biểu diễn sóng dừng cho thí nghiệm này. Chỉ rõ tại màn phản xạ là nút hay bụng sóng. b) Trong thí nghiệm này, khoảng cách giữa hai vị trí liên tiếp mà đầu thu ghi nhận được cường độ sóng cực đại là 14 mm. Xác định bước sóng và tần số của sóng viba này. c) Với phương án thí nghiệm này thì xác định vị trí ứng với nút sóng hay bụng sóng sẽ dễ hơn? Vì sao?


Vận dụng kiến thức đã học về sóng dừng:
- Hiện tượng xuất hiện các điểm đứng yên ở những vị trí xác định khi đang có sóng lan truyền được gọi là hiện tượng sóng dừng.
- Sóng dừng với hai đầu cố định: \(L = k\frac{\lambda }{2}{\rm{ }}\left( {k \in {N^*}} \right)\)
- Số bụng sóng = số bó sóng = k
- Số nút sóng = k + 1.
- Khoảng cách giữa bụng sóng và nút sóng gần nhất:\(\frac{\lambda }{4}\).
- Khoảng cách giữa 2 nút hoặc 2 bụng gần nhất:\(\frac{\lambda }{2}\).

a) Biểu diễn sóng dừng của sóng viba, vị trí màn phản xạ ứng với bụng sóng.
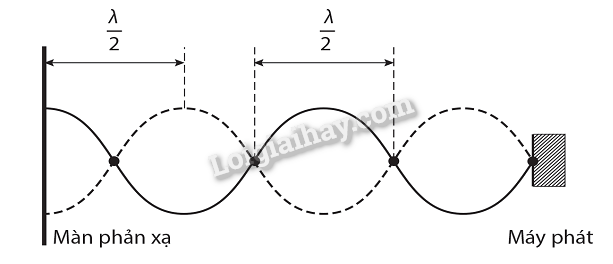
b) Khoảng cách giữa hai vị trí liên tiếp thu được cường độ sóng cực đại là khoảng cách giữa hai bụng sóng và bằng nửa bước sóng. Do đó, bước sóng của sóng này là 28 mm. Sóng viba truyền trong không khí với tốc độ c = 3,0.108 m/s nên tần số của sóng trong thí nghiệm này là: \(f = \frac{c}{\lambda } = \frac{{{{3.10}^8}}}{{{{28.10}^{ - 3}}}} = 1,{1.10^{11}}{\rm{ Hz}}\)
c) Xác định vị trí nút sóng sẽ dễ hơn do cường độ sóng tại đó bằng 0.
