Câu hỏi/bài tập:
1.1
Đề bài:
Chu kì dao động là:
A. Thời gian chuyển động của vật
B. Thời gian vật thực hiện được một dao động toàn phần
C. Số dao động toàn phần mà vật thực hiện được
D. Số dao động toàn phần mà vật thực hiện được trong một giây

Dựa vào lý thuyết về chu kì dao động

Chu kì dao động là khoảng thời gian để vật thực hiện được một dao động toàn phần
Đáp án B
1.2
Đề bài:
Khi vật thực hiện được một dao động tương ứng với pha dao động sẽ thay đổi một lượng:
A. \(0rad\)
B. \(\frac{\pi }{2}rad\)
C. \(\pi rad\)
D. \(2\pi rad\)

Dựa vào lý thuyết về pha dao động

Khi vật thực hiện được một dao động tương ứng với pha dao động sẽ thay đổi một lượng: 2π rad
Đáp án D
1.3
Đề bài:
Chu kì dao động của một vật được xác định bởi biểu thức
A. \(T = 2\pi \omega \)
B. \(T = \frac{{2\pi }}{\omega }\)
C. \(T = \pi \omega \)
D. \(T = \frac{\pi }{\omega }\)

Vận dụng lý thuyết về chu kì dao động

Chu kì dao động của một vật được xác định bởi biểu thức:
\(T = \frac{{2\pi }}{\omega }\)
Đáp án B
1.4
Đề bài:
Đơn vị của tần số dao động trong hệ đơn vị SI là
A. Hz
B. s
C. cm
D. m

Vận dụng lý thuyết về tần số dao động

Đơn vị của tần số dao động trong hệ đơn vị SI là Hz
Đáp án A
1.5
Đề bài:
Một vật đang dao động với chu kì là 0,3s tần số dao động của vật là
A. 0,3 Hz.
B. 0,33 Hz
C. 3,33 Hz.
D. 33 Hz.

Vận dụng công thức tính tần số dao động dựa vào chu kì: \(f = \frac{1}{T}\)

Tần số dao động của vật là:
\(f = \frac{1}{T} = \frac{1}{{0,3}} = 3,33Hz\)
1.6
Đề bài:
Hai vật dao động điều hoà với biên độ dao động khác nhau nhưng có cùng tần số góc, khi đó ta có thể kết luận gì về pha của hai dao động?
A. Hai đao động cùng pha với nhau.
B. Hai dao động ngược pha với nhau
C. Hai dao động vuông pha với nhau
D. Chưa đủ dữ kiện để kết luận

Vận dụng lý thuyết về pha dao động
Advertisements (Quảng cáo)

Khi hai vật dao động điều hoà với cùng tần số góc, độ lệch pha giữa hai dao
động điều hoà không thay đổi theo thời gian nhưng đề bài chưa đủ dữ liệu để
xác định giá trị độ lệch pha.
Đáp án D
1.7
Đề bài:
Trong các dao động đúng mô tả dưới đây, dao động này được xem là dao động tuần hoàn
A. Dao động của con lắc đồng hồ khi đang hoạt động.
B. Lao động của chiếc thuyền trên mặt sông
C. Dao động của quả bóng cao su đang này trên mặt đât.
D. Dao động của dây đàn sau khi được gãy

Vận dụng khái niệm dao động tuần hoàn: Sau những khoảng thời gian bằng nhau, vật trở lại vị trí cũ theo hướng cũ thì dao động của vật đó là tuần hoàn

Dao động của đồng hồ quả lắc được xem như dao động tuần hoàn vì nó dao
động quanh một vị trí cân bằng xác định và chuyển động của nó được lặp lại
sau những khoảng thời gian bằng nhau.
Đáp án A
1.8
Đề bài:
Khi tiến hành thí nghiệm khảo sát vị trí vật nặng của con lắc là xo đang dao động bằng cách sử dụng thước thẳng, bạn học sinh thấy rằng vật nặng dao động từ vị trí 1 cm đến vị trí là 11 cm trên thước. Biên độ dao động của vật nặng trong con lắc lò xo là
A. 10 cm.
B. 6 cm.
C. 5 cm.
D. 12 cm.

Vận dụng công thức tính biên độ của vật \(A = \frac{{\left| {{x_2} - {x_1}} \right|}}{2}\)

Biên độ dao động của vật nặng
\(A = \frac{{\left| {{x_2} - {x_1}} \right|}}{2} = \frac{{\left| {11 - 1} \right|}}{2} = 5cm\)
Đáp án C
1.9
Đề bài:
Một bạn học sinh quan sát thấy con lắc trong đồng hồ quả lắc thực hiện được 20 dao động trong 30 giây. Dao động của con lắc trong đồng hồ này có đặc điểm nào sau đây?
A. Dao động điều hòa, tần số là 1,5 Hz.
B. Dao động điều hoà, tần số là 0,7 Hz.
C. Dao động tuần hoàn, tần số là 1,5 Hz.
D. Dao động tuần hoàn, tần số là 0,7 Hz.

Vận dụng công thức tính tần số dao động: \(f = \frac{N}{t}\)

Dao động của con lắc là dao động tuần hoàn có tần số
\(f = \frac{N}{t} = \frac{{20}}{{30}} = 0,7Hz\)
Đáp án D
1.10
Đề bài:
Các nhà thực nghiệm đo được tần số dao động của một hệ gồm thanh silicon siêu nhỏ có virus dính trên đó đang thực hiện dao động là 2,87.1014 Hz. Tần số góc của hệ dao động trên bằng bao nhiêu?
A. 1,89.1015 rad/s.
B. 3,48.1015 rad/s.
C. 2,18.1014 rad/s.
D. 4,57.1014 rad/s.

Vận dụng công thức tính tần số góc: \(\omega = 2\pi f\)

Tần số góc của hệ dao động
\(\omega = 2\pi f = 2\pi .2,{87.10^{14}} = 1,{8.10^{15}}rad/s\)
1.11
Đề bài:
Hai vật dao động điều hoà có li độ được biểu diễn trên đồ thị li độ –thời gian như Hình 1.1. Phát biểu nào dưới đây mô tả đúng tính chất của hai vật?
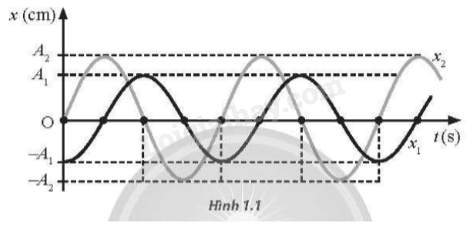
A. Hai vật dao động cùng tần số, cùng pha.
B. Hai vật dao động cùng tần số, vuông pha
C. Hai vật dao động khác tần số, cùng pha.
D. Hai vật dao động khác tần số, vuông pha

Dựa vào phương pháp đồ thị đọc đồ thị li độ theo thời gian

Dựa vào trục Ot, ta thấy hai vật có cùng chu kì, nên hai vật có cùng tần số. Xét thời điểm ban đầu, vật 1 xuất phát từ vị trí cân bằng, vật 2 xuất phát từ biên âm, do đó hai vật dao động vuông pha nhau.
Đáp án B
