Trắc nghiệm trang 9, 10, 11, 12, 13 SBT Vật lý 11 - Chân trời sáng tạo: Một vật thực hiện dao động điều hoà có li độ phụ thuộc vào thời gian theo biểu thức A. \(x = A{t^2}\) B...

2.1

Đề bài:

Một vật thực hiện dao động điều hoà có li độ phụ thuộc vào thời gian theo biểu thức

A. \(x = A{t^2}\)

B. \(x = A\cos (\omega t + {\varphi _0})\)

C. \(x = {v_0}t\)

D. \(x = {v_0}t + \frac{1}{2}a{t^2}\)

Vận dụng lý thuyết về phương trình li độ theo thời gian của dao động điều hòa

Một vật thực hiện dao động điều hoà có li độ phụ thuộc vào thời gian theo biểu thức \(x = A\cos (\omega t + {\varphi _0})\)

Đáp án B

2.2

Đề bài:

Một chất điểm dao động điều hoà với phương trình li độ \(x = 3\cos (2\pi t + \frac{\pi }{4})\) (cm). Pha ban đầu của dao động trên là

A. 3 rad

B. 2π rad

C. \(\frac{\pi }{4}\) rad

D. \((2\pi t + \frac{\pi }{4})\) rad

Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + {\varphi _0}} \right)\)với:

+ \(x\) là li độ dao động.

+ \(A\) là biên độ dao động.

+ \(\omega \) là tần số góc của dao động.

+ \(\left( {\omega t + {\varphi _0}} \right)\) là pha của dao động ở thời điểm t.

+\({\varphi _0}\) là pha ban đầu.

Pha ban đầu của dao động trên là \({\varphi _0} = \frac{\pi }{4}\) rad

Đáp án C

2.3

Đề bài:

Quãng đường một vật đi được trong một chu kì dao động điều hoà là 24 cm. Biên độ dao động của vật là

A. 24cm

B. 12 cm

C. 6cm

D. 8cm

Quãng đường vật đi được trong một chu kì dao động bằng 4 lần biên độ.

Biên độ dao động của vật là: \(s = 4A \Rightarrow A = \frac{s}{4} = \frac{{24}}{4} = 6cm\)

Đáp án C

2.4

Đề bài:

Trong dao động điều hoà, vận tốc và gia tốc biến thiên điều hoà theo thời gian và có cùng

A. biên độ.

B. tần số

C. pha ban đầu

D. pha

Vận dụng lý thuyết về vận tốc và gia tốc trong dao động điều hòa

Trong dao động điều hoà, vận tốc và gia tốc biến thiên điều hoà theo thời gian và có cùng tần số, tần số góc, chu kì.

Đáp án B

2.5

Đề bài:

Một vật cho động điều hoà theo một trục cố định. Phát biểu nào dưới đây là không chính xác

A. Quãng đường vật đi được trong một chu kì dao động bằng 4 lần biên độ

B. Đồ thị li độ theo thời gian của vật là một đường hình sin

C. Chiều dài quỹ đạo chuyển động của vật bằng 2 lần biên độ

D. Quỹ đạo chuyển động của vật là một đường hình sin

Vận dụng lý thuyết về dao động điều hòa

Đối với vật dao động điều hòa:

+ Quỹ đạo chuyển động là một đoạn thẳng

+ Li độ biến thiên theo thời gian theo hàm sin (hoặc cos)

Đáp án D

2.6

Đề bài:

Một chất điểm dao động điều hoà trên trục Ox có phương trình li độ \(x = 8\cos (\pi t + \frac{\pi }{a})\) ( x tính bằng cm, t tính bằng s) thì:

(1) lúc t=0 s, chất điểm chuyển động theo chiều âm của trục Ox.

(2) chất điểm chuyển động trên đoạn thẳng dài 16 cm.

(3) chu kì dao động là 4 s.

(4) vận tốc chất điểm khi qua vị trí cân bằng là 8 cm/s.

(5) gia tốc của chất điểm cực đại tại vị trí x = 8 cm.

Trong các phát biểu trên, số phát biểu đúng là

A. 1

B. 2

C. 3

D. 4

Vận dụng phương trình li độ, vận tốc và gia tốc trong dao động điều hòa

Các phát biểu đúng: (1), (2), (5).

(1) – đúng vì pha ban đầu lớn hơn 0

(2) – đúng vì L = 2A = 16 cm

(3) – sai vì \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{\pi } = 2s\)

(4) – sai vì v_max=Aω=8π cm/s

(5) – sai vì a_max=Aω²=8π² cm/s²

Đáp án C

2.7

Đề bài:

Trong dao động điều hoà, phát biểu nào dưới đây là không chính xác

(1) Ở vị trí biên âm, gia tốc có giá trị cực tiểu, vận tốc bằng 0.

(2) Ở vị trí biên âm, gia tốc có giá trị cực đại, vận tốc bằng 0.

(3) Ở vị trí cân bằng, gia tốc có giá trị cực đại, vận tốc bằng 0.

(4) Ở vị trí cân bằng, gia tốc bằng 0, vận tốc có độ lớn cực đại.

(5) Ở vị trí biên dương, gia tốc có giá trị cực tiểu, vận tốc bằng 0.

(6) Ở vị trí biên dương, gia tốc có giá trị cực đại, vận tốc bằng 0.

A. (1), (3), (6).

B. (2), (5), (6).

C. (2), (4), (5).

D. (3), (4), (5).

Vận dụng lý thuyết về dao động điều hòa

(1) – sai vì ở biên âm gia tốc có giá trị cực đại

(3) – sai vì ở VTCB gia tốc bằng 0

(6) – sai vì ở biên dương gia tốc có giá trị cực tiểu.

Đáp án A

2.8

Đề bài:

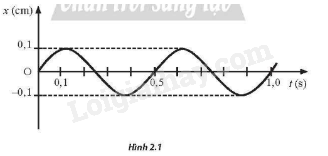
Một vật dao động điều hoà có đô thị li độ – thời gian như Hình 2.1. Tại thời điểm t = 0,5 s, vận tốc của vật có độ lớn là

A. \(\frac{\pi }{5}cm/s\)

B. \(\frac{{2\pi }}{5}cm/s\)

C. \(\frac{{3\pi }}{5}cm/s\)

D. \(\frac{{4\pi }}{5}cm/s\)

Dựa vào đồ thị suy ra A và T

Tại t=0,5 s, vật ở vị trí cân bằng.

\(v = {v_{\max }} = \omega A = \frac{{2\pi A}}{T} = \frac{{2\pi .0,1}}{{0,5}} = \frac{{2\pi }}{5}cm/s\)

2.9

Đề bài:

Một chất điểm dao động điều hoà với phương trình vận tốc \(v = 2\sqrt 2 \cos (2t + \frac{{2\pi }}{5})\) (cm/s). Tại thời điểm vật có vận tốc tức thời là 2 cm/s thi li độ của vật có thể là

A. 1 cm.

B. \(\sqrt 2 \) cm.

C. 2 cm.

D. \(2\sqrt 2 \)cm.

Áp dụng công thức độc lập với thời gian tính li độ

Ta có:

\(A = \frac{{{v_{\max }}}}{\omega } = \frac{{2\sqrt 2 }}{2} = \sqrt 2 cm\)

\(\begin{array}{l}{\left( {\frac{v}{{{v_{\max }}}}} \right)^2} + {\left( {\frac{x}{A}} \right)^2} = 1\\ \Rightarrow {x^2} = {A^2}\left( {1 - {{\left( {\frac{v}{{{v_{\max }}}}} \right)}^2}} \right) = {\left( {\sqrt 2 } \right)^2}\left( {1 - {{\left( {\frac{2}{{2\sqrt 2 }}} \right)}^2}} \right) = 1cm\\ \Rightarrow x = 1cm\end{array}\)

Đáp án A

2.10

Đề bài:

Một chất điểm dao động điều hoà trên trục Ox, gốc toạ độ O tại vị trí cân bằng. Biết phương trình vận tốc của chất điểm là: \(v = 10\pi \cos \left( {\pi t + \frac{{5\pi }}{6}} \right)cm/s\). Phương trình li độ của chất điểm có dạng là

A. \(x = 10\cos \left( {\pi t + \frac{\pi }{3}} \right)\)cm

B. \(x = 10\cos \left( {\pi t - \frac{\pi }{3}} \right)\)cm

C. \(x = 10\cos \left( {\pi t + \frac{{5\pi }}{6}} \right)\)cm

D. \(x = 10\cos \left( {\pi t + \frac{{4\pi }}{3}} \right)\)cm

Phương trình vận tốc tổng quát có dạng:

\(v = - A\omega \sin \left( {\omega t + {\varphi _0}} \right) = A\omega \cos \left( {\omega t + {\varphi _0} + \frac{\pi }{2}} \right)\) suy ra phương trình li độ

Phương trình vận tốc tổng quát có dạng:

\(v = - A\omega \sin \left( {\omega t + {\varphi _0}} \right) = A\omega \cos \left( {\omega t + {\varphi _0} + \frac{\pi }{2}} \right)\)

Ta có: A = 10 cm, \(\omega = \pi rad/s\), \({\varphi _0} + \frac{\pi }{2} = \frac{{5\pi }}{6} \Rightarrow {\varphi _0} = \frac{\pi }{3}rad\)

Phương trình li độ của chất điểm là:

\(x = A\cos \left( {\omega t + {\varphi _0}} \right) = 10\cos \left( {\pi t + \frac{\pi }{3}} \right)cm\)

Đáp án A

2.11

Đề bài:

Xét một vật dao động điều hoà, trong một chu kì dao động vật đi được quãng đường 20 cm. Trong 2 phút, vật thực hiện được 120 dao động. Tại thời điểm ban đầu, vật đi qua vị trí có li độ 2,5 cm và đang hướng về vị trí cân bằng. Phương trình vận tốc của vật có dạng là

A. \(v = 10\pi \cos \left( {2\pi t - \frac{{5\pi }}{6}} \right)cm/s\)

B. \(v = 10\pi \cos \left( {2\pi t + \frac{{5\pi }}{6}} \right)cm/s\)

C. \(v = 5\pi \cos \left( {2\pi t - \frac{{5\pi }}{6}} \right)cm/s\)

D. \(v = 5\pi \cos \left( {2\pi t + \frac{{5\pi }}{6}} \right)cm/s\)

Phương trình vận tốc tổng quát có dạng:

\(v = - A\omega \sin \left( {\omega t + {\varphi _0}} \right) = A\omega \cos \left( {\omega t + {\varphi _0} + \frac{\pi }{2}} \right)\)

Ta có: S = 4A = 20 => A = 5 cm

\(T = \frac{{\Delta t}}{N} = \frac{{120}}{{120}} = 1s \Rightarrow \omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{1} = 2\pi rad/s\)

Tại thời điểm t = 0:

\({x_0} = A\cos {\varphi _0} \Rightarrow \cos {\varphi _0} = \frac{{2,5}}{5} = \frac{1}{2}\) (1)

\({v_0} 0\) (2)

Từ (1) và (2) \( \Rightarrow {\varphi _0} = \frac{\pi }{3}rad\)

Phương trình vận tốc của vật là:

\(v = A\omega \cos \left( {\omega t + {\varphi _0} + \frac{\pi }{2}} \right) = 10\pi \cos \left( {2\pi t + \frac{{5\pi }}{6}} \right)cm/s\)