Tự luận trang 23, 24, 25, 26 SBT Vật lý 11 - Chân trời sáng tạo: Một tín hiệu của sóng siêu âm được gửi đi từ một chiếc tàu xuống đáy biển theo phương thẳng dung. Sau 0,8 giây...

6.1

Đề bài:

Một tín hiệu của sóng siêu âm được gửi đi từ một chiếc tàu xuống đáy biển theo phương thẳng dung. Sau 0,8 giây, tàu nhận được tín hiệu phản xạ từ đáy biển. Cho biết tốc độ truyền của sóng siêu âm trong nước biển bằng 1,6.103 m/s. Độ sâu của đáy biển tại nơi khảo sát bằng bao nhiêu?

Phương pháp giải

Áp dụng công thức tính quãng đường

\(2d = vt \Rightarrow d = \frac{{1600.0,8}}{2} = 640m\)

6.2

Đề bài:

Sóng nước truyền trên một mặt hồ có phương trình: u=3,2cos(8,5t – 0,5x) (cm) (x được tính bằng em, t được tính bằng s). Tỉnh tốc độ của sóng truyền trên mặt hồ.

Phương pháp giải

Vận dụng phương trình truyền sóng

Ta có:

\(\begin{array}{l}\frac{{2\pi }}{T} = 8,5 \Rightarrow T = 0,74s\\\frac{{2\pi x}}{\lambda } = 0,5x \Rightarrow \lambda = 12,6cm\\\lambda = vT \Rightarrow v = \frac{\lambda }{T} = \frac{{12,6}}{{0,74}} = 17,03cm/s\end{array}\)

6.3

Đề bài:

Hình 6.2 là hình ảnh của một sóng trên dây đàn hồi tại một thời điểm xác định. Cho biết thời gian ngắn nhất để điểm A từ vị trí cân bằng dao động theo phương thẳng đứng và trở lại vị trí này là 0,25 s và khoảng cách AB bằng 40 cm

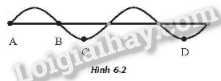
a) Tính tốc độ truyền sóng trên dây.

b) Khoảng cách CD bằng bao nhiêu

Phương pháp giải

Quan sát sóng trên dây

a) Ta có:

\(\begin{array}{l}\frac{T}{2} = 0,25s \Rightarrow T = 0,5s\\\frac{\lambda }{2} = 40cm \Rightarrow \lambda = 80cm\end{array}\)

\(\lambda = vT \Rightarrow v = \frac{\lambda }{T} = \frac{{80}}{{0,5}} = 160cm/s\)

b) CD= λ =80 cm

6.4

Đề bài:

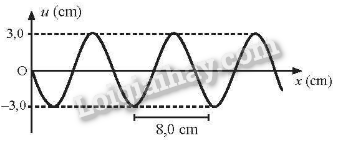
Hình 6.3 là đô thị li độ – khoảng cách của một sóng truyền dọc theo phương Ox tại một thời điểm xác định. Cho biết khoảng cách giữa hai đỉnh sóng liên tiếp bằng 8,0 cm và thời gian sóng truyền giữa hai đỉnh nảy bằng 0.02 s. Thiết lập phương trình truyền sóng của sóng này.

Phương pháp giải

Quan sát đồ thị

Ta có: \(v = \frac{8}{{0,02}} = 400cm/s\)

Dựa vào đồ thị ta có: \(\lambda = \frac{{400}}{f} = 8 \Rightarrow f = 50Hz\)

Phương trình truyền sóng: \(u = 3\cos \left( {100\pi t - \frac{{\pi x}}{4}} \right)cm\)

6.5

Đề bài:

Hình 6.4 là đô thị li độ — khoảng cách của một sóng truyền dọc trên một sợi dây tại một thời điểm xác định. Cho biết biên độ sóng bằng 0,40 cm và khoảng cách giữa hai đỉnh sóng liên tiếp trên dây băng 25,0 cm. Tốc độ truyền sóng trên dây bằng 80,0 cm/s.

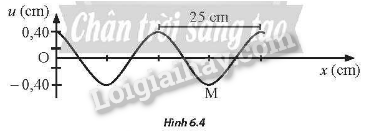
a) Sau khoảng thời gian ngắn nhất bằng bao nhiêu thì điểm M lại hạ xuống thấp nhất một lần nữa?

b) Tỉnh thời gian ngắn nhất kể từ lúc điểm M hạ xuống thấp nhất đến khi điểm M có li độ bằng 0,20 cm

Phương pháp giải

Dựa vào đồ thị

a) Ta có: \(T = \frac{\lambda }{v} = \frac{{0,25}}{{0,8}} = 0,31s\)

Vậy sau 0,31 s thì điểm M lại hạ xuống thấp nhất một lần nữa

b) \(t = \frac{T}{3} = \frac{{0,31}}{3} = 0,1s\)

6.6

Đề bài:

Một còi báo động phát sóng âm trong một môi trường đẳng hướng. Tại vị trí cách còi một khoảng bằng 75,0 m, cường độ âm đo được bằng 0,010 W/m2. Ở khoảng cách 15,0 m, cường độ ẩm bằng bao nhiêu?

Phương pháp giải

Vận dụng công thức tính cường độ âm

Ta có: \({I_1} = \frac{P}{{4\pi r_1^2}};{I_2} = \frac{P}{{4\pi r_2^2}} \Rightarrow \frac{{{I_1}}}{{{I_2}}} = \frac{{r_2^2}}{{r_1^2}} \Rightarrow {I_2} = {I_1}\frac{{r_1^2}}{{r_2^2}} = 0,01.{\left( {\frac{{75}}{{15}}} \right)^2} = 0,25W/{m^2}\)

Vậy ở khoảng cách 15,0 m, cường độ ẩm bằng 0,25 W/m²

6.7

Đề bài:

Một sóng ngang truyền dọc trên một dây đàn hồi dài AB = 25 cm, hai điểm gần nhất trên dây dao động cùng pha nhau, cách nhau 4 cm. Dọc theo dây này, có bao nhiêu điểm dao động cùng pha và bao nhiêu điểm dao động ngược pha với đầu A của dây?

Phương pháp giải

Vận dụng kiến thức dao động cùng pha, ngược pha

Hai điểm gần nhất trên dây dao động cùng pha nhau, cách nhau 4 cm nên bước sóng là 4 cm.

Điểm M dao động cùng pha với A:

MA=k λ = 4k ≤ AB⇒k ≤6,25

=> k=1;2;3;4;5;6 (không chọn k = 0 vì khi đó M trùng với A). Vậy có 6 điểm dao động cùng pha với A.

Điểm M dao động ngược pha với A:

\(MA = \left( {k + \frac{1}{2}} \right)\lambda = 4k + 2 \le AB \Rightarrow k \le 5\)

=> k=0;1;2;3;4;5 Có 6 điểm dao động ngược pha với A.

6.8

Đề bài:

Một sóng có tần số 50 Hz truyền trong một môi trường đồng chất. Tại một thời điểm, hai điểm gần nhất trên cùng một phương truyền sóng dao động lệch pha nhau \(\frac{\pi }{2}\) cách nhau 60 cm. Tính độ lệch pha

a) giữa hai điểm cách nhau 480 cm tại cùng một thời điểm

b) tại một điểm trong môi trường sau khoảng thời gian 0,01 s.

Phương pháp giải

Vận dụng kiến thức pha dao động

Độ lệch pha của hai điểm tại hai thời điểm t₁ và t₂; cách nhau một khoảng d:

\(\left( {\omega {t_2} - \frac{{2\pi {d_2}}}{\lambda }} \right) - \left( {\omega {t_1} - \frac{{2\pi {d_1}}}{\lambda }} \right) = \omega \Delta t - \frac{{2\pi d}}{\lambda }\)

Tại cùng một thời điểm Δt = 0; theo đề bài: \(\frac{{2\pi d}}{\lambda } = \frac{\pi }{2} + k\pi \)

Hai điểm gần nhất tương ứng với k=0 => λ=4d=4.60=240 cm

a) Tại cùng một thời điểm: Δt = 0 độ lệch pha:

\(\frac{{2\pi d}}{\lambda } = \frac{{2\pi .480}}{{240}} = 4\pi \)

Suy ra hai điểm này dao động cùng pha.

(Ta thấy: d= 480 = 2λ =kλ hai điểm dao động cùng pha)

b) Tại một điểm d1=d2 nên độ lệch pha

ωΔt=2π.50.0,01=π

=> Hai dao động ngược pha

6.9

Đề bài:

Xét tại vị trí M cách nguồn âm điểm (nguồn phát sóng âm trong môi trường đồng chất, đẳng hướng) một khoảng 200 m, cường độ âm đo được bằng 6,0.10^-5 W/m²

a) Tính công suất của nguồn âm này

b) Cho biết công suất được thu nhận ở bề mặt một micro đặt tại vị trí M là 4,50.10^-9 W. Tỉnh diện tích bề mặt của micro này

Phương pháp giải

Vận dụng công thức tính công suất

a) Ta có: P=I.4πr²=6,00.10⁻⁵.4π.(200)²≈30,2W

b) Diện tích bề mặt của micro:

\(S = \frac{{P’}}{I} = \frac{{4,{{5.10}^{ - 9}}}}{{{{6.10}^{ - 5}}}} = 0,75c{m^2}\)

6.10

Đề bài:

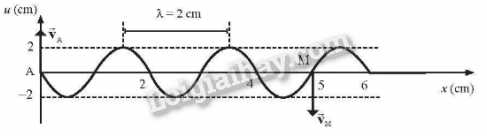
Một dây AB rất dài căng ngang (coi khối lượng dây là không đáng kể) có đầu A dao động điều hòa thẳng đứng với biên độ 2,0 cm và tần số 0,5 Hz. Sau 5,0 s kể từ khi A bắt đầu đao động, điểm M trên dây cách A một đoạn 5,0 cm cũng bắt đầu dao động.

a) Viết phương trình dao động của A. Chọn gốc thời gian là khi A bắt đầu dao động tử vị trí cân bằng theo chiều dương.

b) Suy ra phương trình dao động của M.

c) Vẽ hình dạng của dây vào thời điểm 6,0 s kể từ khi A bắt đầu dao động.

Phương pháp giải

Vận dụng phương trình sóng

a) Phương trình dao động của A:

\({u_A} = 2\cos \left( {\pi t - \frac{\pi }{2}} \right)cm\)

b) Ta có: \(v = \frac{5}{5} = 1cm/s \Rightarrow \lambda = \frac{1}{{0,5}} = 2cm\)

\({u_M} = 2\cos \left( {\pi t - \frac{\pi }{2} - 2\pi \frac{5}{2}} \right) = 2\cos \left( {\pi t + \frac{{3\pi }}{2}} \right)cm(t \ge 5s)\)

c) \({u_M} = 2\cos \left( {\pi .6 - \frac{\pi }{2} - 2\pi \frac{x}{2}} \right) = 2\cos \left( {\pi x + \frac{\pi }{2}} \right)cm(x \le 6cm)\)

Dây có hình dạng như sau: