Câu hỏi/bài tập:
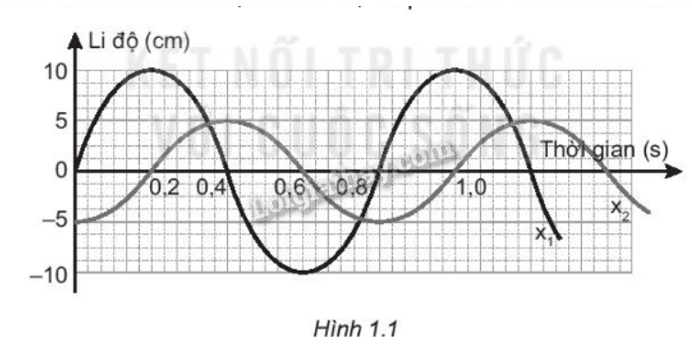
Đồ thị li độ theo thời gian x1, x2, của hai chát điểm dao động điều hoà được mô tả như Hình 1.1. Xác định biên độ và pha ban đầu của mỗi dao động.

- Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\).
- Đồ thị dao động điều hoà.
 :
:
Từ đồ thị ta thấy:
Xét \({x_1}\)
- Biên độ dao động là giá trị lớn nhất của li độ:\(A = x\max = 10\left( {cm} \right)\)
Advertisements (Quảng cáo)
- Lúc t=0, con lắc đang ở VTCB : \(x = 0\) và \(v > 0\)
=> \(x = A\cos \varphi \) \(\cos \varphi = 0 = > \varphi = - \frac{\pi }{2}\)
Vậy dao động \({x_1}\)có :
- Biên độ dao động :\(A = 10\left( {cm} \right)\)
- Pha ban đầu \(\varphi = - \frac{\pi }{2}\)
Xét \({x_2}\)
- Biên độ dao động là giá trị lớn nhất của li độ: \(A = x\max = 5\left( {cm} \right)\)
- Lúc t=0, con lắc đang ở biên âm \(x = - A = - 5\left( {cm} \right)\) và \(v > 0\)
=> \(x = A\cos \varphi \) \(\cos \varphi = - 1 = > \varphi = \pi \)
Vậy dao động \({x_2}\)có :
- Biên độ dao động :\(A = 5\left( {cm} \right)\)
- Pha ban đầu \(\varphi = \pi \)
