Câu hỏi/bài tập:
Một chất điểm dao động điều hoà có phương trình li độ theo thời gian
\(x = 10\cos \left( {\frac{\pi }{3}t + \frac{\pi }{2}} \right)\left( {cm} \right)\). Tại thời điểm t vật có li độ 6 cm và đang hướng về vị trí cân bằng. Sau 9 s kể từ thời điểm t thì vật đi qua li độ:
A. 3 cm đang hướng về vị trí cân bằng.
B.\( - 3\) cm đang hướng về vị trí biên.
C. 6 cm đang hướng về vị trí biên.
D. \( - 6\) cm đang hướng về vị trí cân bằng.

Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với:
+ \(x\) là li độ dao động.
+ \(A\) là biên độ dao động.
+ \(\omega \) là tần số góc của dao động.
Advertisements (Quảng cáo)
+ \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t.
+\(\varphi \) là pha ban đầu.
Chu kì: T là khoảng thời gian để vật thực hiện được một dao động.
Tần số: f là số dao động mà vật thực hiện được trong một giây \(f = \frac{1}{T}\)
Đơn vị của tần số là Héc (Kí hiệu Hz)
Tần số góc \(\omega = \frac{{2\pi }}{T} = 2\pi f(rad/s)\)
 :
:
Từ phương trình ta có :\(\omega = \frac{\pi }{3} = > T = \frac{{2\pi }}{\omega } = \frac{{2\pi .3}}{\pi } = 6(s)\)
Tại thời điểm t vật có li độ 6 cm và đang hướng về vị trí cân bằng
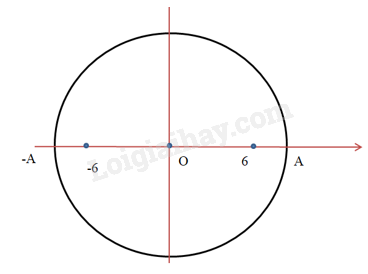
=> sau \(t = 9(s) = \frac{9}{6}T = 1,5T\) \( = T + \frac{T}{2}\) thì vật ở có li độ bằng -6 cm và đang hướng về VTCB
Đáp án 😀
