Câu hỏi/bài tập:
Đồ thị li độ theo thời gian \({x_1},{x_2}\) của hai chất điểm dao động điều hoà được mô tả như Hình 2.2:
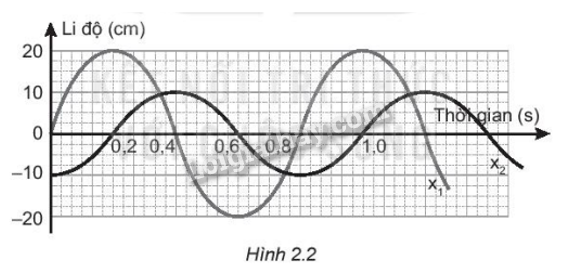
a) Xác định độ lệch pha của hai dao dao động.
b) Viết phương trình dao động của \({x_1},{x_2}\)

:
1. Vận dụng kiến thức đã học trong phần 1. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Đồ thị dao động điều hoà.
2. Độ lệch pha giữa hai dao động cùng chu kì
- Độ lệch pha là đại lượng không đổi, không phụ thuộc vào thời điểmquan sát
\({\varphi _1} > {\varphi _2}\)thì dao động 1 sớm pha hơn dao động 2
\({\varphi _1} < {\varphi _2}\)thì dao động 1 trễ pha hơn dao động 2
\({\varphi _1} = {\varphi _2}\)thì dao động 1 cùng (đồng) pha với dao động 2
\({\varphi _1} = {\varphi _2} + \varphi \) thì dao động 1 ngược pha với dao động 2
 :
:
a) Từ đồ thị ta có :
Tại thời điểm t=0 , vật \({x_1}\) ở vị trí cân bằng \(x = 0\)
Advertisements (Quảng cáo)
=> \({x_1} = {A_1}\cos {\varphi _1} \cos {\varphi _1} = 0 = > {\varphi _1} = \frac{\pi }{2}\)
Biên độ dao động của \({x_2}\): \(A = x\max = 10(cm)\)
Tại thời điểm t=0 , vật \({x_2}\) ở vị trí biên âm \(x = - A\)
\( = > {x_2} = A\cos {\varphi _2} \cos {\varphi _2} = - 1 = > {\varphi _2} = \pi \)
=> độ lệch pha của hai dao dao động \(\Delta \varphi = \ {{\varphi _2} - {\varphi _1}} \ = \frac{\pi }{2}\)
=> hai dao động vuông pha với nhau hoặc x1 sớm pha hơn x2 là \(\Delta \varphi = \frac{\pi }{2}\)
b) Từ đồ thị ta có :
Xét \({x_1}\)
Biên độ dao động của \({x_1}\) : \(A = x\max = 20(cm)\)
Từ vị trí thấp nhất đến vị trí cao nhất là \(\frac{T}{2} = 0,4 = > T = 0,8(s)\)\( = > \omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,8}} = 2,5\pi \)(rad/s)
Tại t = 0 vật có li độ x = 0 và đang chuyển động theo chiều dương nên \({\varphi _1} = - \frac{\pi }{2}\)
=> Phương trình dao động \({x_1} = 20\cos \left( {2,5\pi t - \frac{\pi }{2}} \right)\)
Xét \({x_2}\)
Biên độ dao động của \({x_2}\) : \(A = x\max = 10(cm)\)
Từ vị trí thấp nhất đến vị trí cao nhất là \(\frac{T}{2} = 0,4 = > T = 0,8(s)\)\( = > \omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,8}} = 2,5\pi \)(rad/s)
Tại t = 0 vật có li độ x = -10 cm và đang chuyển động theo chiều dương nên \({\varphi _2} = - {\pi }\)
=> Phương trình dao động \({x_2} = 10\cos \left( {2,5\pi t - \pi } \right)\)
