Câu hỏi/bài tập:
Cho mạch điện như Hình 23.6. Cho biết cáo giá trị điện trở: \({R_1} = 4\Omega \),
\({R_2} = {R_5} = 20\Omega \), \({R_3} = {R_6} = 12\Omega \),\({R_4} = {R_7} = 8\Omega \). Hiệu điện thể giữa hai đầu đoạn
mạch \({U_{AB}} = 48V\)
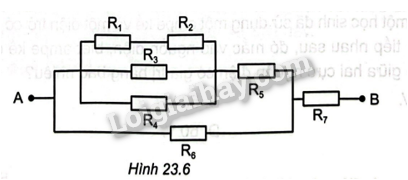
a) Tính điện trở \({R_{AB}}\) của đoạn mạch AB.
b) Tìm cường độ dòng điện và hiệu điện thể của mỗi điện trở.

Vận dụng kiến thức định luật Ohm trong các đoạn mạch .

a) Ta có \({R_1}nt{R_2} = > {R_{12}} = {R_1} + {R_2} = 4 + 20 = 24\Omega \)
\({R_3}//{R_4} = > {R_{34}} = \frac{{{R_3}.{R_4}}}{{{R_3} + {R_4}}} = 4.8\Omega \) và ta có \({R_{12}}//{R_{34}} = > {R_{1234}} = 4\Omega \)
Advertisements (Quảng cáo)
Ta lại có : \({R_5}nt{R_{1234}} = > {R_{12345}} = {R_5} + {R_{1234}} = 4 + 20 = 24\Omega \)
Tương tự \({R_6}//{R_{12345}} = > {R_{123456}} = 8\Omega \) và \({R_7}nt{R_{123456}}\)=> điện trở \({R_{AB}}\) của đoạn mạch AB \({R_{AB}} = {R_7} + {R_{123456}} = 8 + 8 = 16\Omega \)
b) ta có \({I_{AB}} = \frac{{{U_{AB}}}}{{{R_{AB}}}} = \frac{{48}}{{16}} = 3A\) mà \({R_7}nt{R_{123456}} = > {I_7} = {I_{123456}} = 3A\)
=> hiệu điện thế \({U_7} = {I_7}.{R_7} = 3.8 = 24V\)
Ta có \({U_{123456}} = {U_{AB}} - {U_7} = 48 - 24 = 24V\)mà ta có \({R_6}//{R_{12345}} = > {U_6} = {U_{12345}} = 24V\)
=> Cường độ dòng điện : \({I_6} = \frac{{{U_6}}}{{{R_6}}} = \frac{{24}}{{12}} = 2A\)
Ta có : \({I_{12345}} = \frac{{{U_{12345}}}}{{{R_{12345}}}} = \frac{{24}}{{24}} = 1A\)mà \({R_5}nt{R_{1234}} = > {I_5} = {I_{1234}} = 1A\)
=> hiệu điện thế \({U_5} = {I_5}.{R_5} = 1.20 = 20V = > {U_{1234}} = {U_{12345}} - {U_5} = 24 - 20 = 4V\)
Mà \({R_{12}}//{R_{34}} = > {U_{12}} = {U_{34}} = 4V\) mà => \({I_3} = \frac{{{U_3}}}{{{R_3}}} = \frac{4}{{12}} = \frac{1}{3}A\) và \({I_4} = \frac{{{U_4}}}{{{R_4}}} = \frac{4}{8} = \frac{1}{2}A\)
Ta có \({I_{12}} = \frac{{{U_{12}}}}{{{R_{12}}}} = \frac{4}{{24}} = \frac{1}{6}A\) mà \({R_1}nt{R_2} = > {I_1} = {I_2} = \frac{1}{6}A\)
=> \({U_1} = {I_1}.{R_1} = \frac{1}{6}.4 = \frac{2}{3}V\) và \({U_2} = {I_2}.{R_2} = \frac{1}{6}.20 = \frac{{10}}{3}V\)
