Câu hỏi/bài tập:
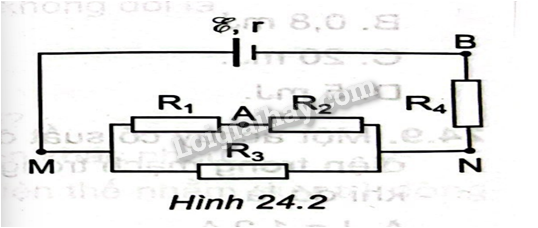
Cho mạch điện có sơ đồ như Hình 24.2. Trong đó: \(\xi = 1,2V\), \(r = 0,5\Omega \) , \({R_1} = {R_3} = 2\Omega \), \({R_2} = {R_4} = 4\Omega \). Tính hiệu điện thế giữa hai điểm A, B.

Định luật Ohm trong các đoạn mạch.
Công thức tính suất điện động \(\xi = I(R + r)\)
Lời giải chi tiết :
Từ hình vẽ ta có : \([({R_1}nt{R_2})//{R_3}]nt{R_4}\)
Advertisements (Quảng cáo)
=> \({R_{12}} = {R_1} + {R_2} = 2 + 4 = 6\Omega \) và \({R_{123}} = \frac{{{R_{12}}.{R_3}}}{{{R_{12}} + {R_3}}} = \frac{{6.2}}{{6 + 2}} = 1,5\Omega \)
=> Điện trở của mạch ngoài \({R_N} = {R_{123}} + {R_4} = 1,5 + 4 = 5,5\Omega \)
=> Cường độ dòng điện của mạch chính : \(I = \frac{\xi }{{{R_N} + r}} = \frac{{1,2}}{{5,5 + 0,5}} = 0,2A\)
=> cường độ dòng điện qua điện trở \({R_4}\): \({I_4} = I = 0,2A = > {U_4} = {I_4}.{R_4} = 0,2.4 = 0,8V\)
=>\({U_{12}} = {U_3} = I.{R_N} - {U_4} = 0,2.5,5 - 0,8 = 0,3V\)=> \({I_{12}} = \frac{{{U_{12}}}}{{{R_{12}}}} = \frac{{0,3}}{6} = 0,05A = {I_1} = {I_2}\)
=> hiệu điện thế qua điện trở \({R_2}\) là : \({U_2} = {I_2}{R_2} = 0,05.4 = 0,2V\)
=> hiệu điện thế giữa hai điểm A, B \({U_{AB}} = {U_{AN}} + {U_{NB}} = {U_2} + {U_4} = 0,2 + 0,8 = 1V\)
