Câu hỏi/bài tập:
Hình 3.1 mô tả sự biến thiên vận tốc theo thời gian của một vật dao động điều hoà.
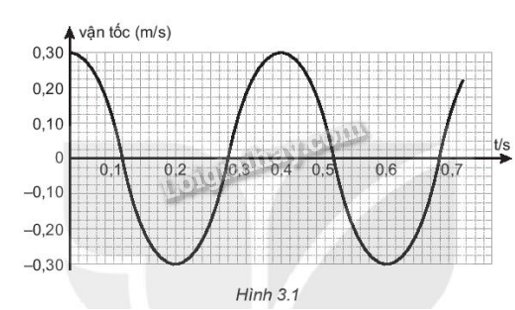
a) Viết phương trình vận tốc theo thời gian.
b) Viết phương trình li độ và gia tốc theo thời gian.

:
Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Phương trình của vận tốc có dạng : \(v = A\omega \cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right)\)
- Khi vật ở VTCB : \(v = \pm \omega A\)
- Khi vật ở vị trí biên : \(v = 0\)
Phương trình của gia tốc có dạng : \(a = A{\omega ^2}\cos \left( {\omega t + \varphi + \pi } \right)\)
- Khi vật ở VTCB : \(a = 0\)
- Khi vật ở vị trí biên : \(a = \pm {\omega ^2}A\)
Advertisements (Quảng cáo)
 :
:
a) Dựa vào đồ thị ta có :
Thời gian từ thời điểm thấp nhất đến điểm cao nhất : \(\frac{T}{2} = 0,2s = > T = 0,4s = > \omega = \frac{{2\pi }}{T} = 5\pi (rad/s)\)
Vận tốc cực đại của dao động :
\(v\max = A\omega = 30(m/s) = > A = \frac{{v\max }}{\omega } = \frac{6}{\pi }(cm)\)
Tại thời điểm t=0 , vật có v=vmax => vật ở VTCB và v > 0
=> x=0 => \(\cos \varphi = 0 = > \varphi = - \frac{\pi }{2}\)
Phương trình của vận tốc có dạng : \(v = A\omega \cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right)\)
\( = > v = \frac{6}{\pi }.5\pi \cos \left( {5\pi t - \frac{\pi }{2} + \frac{\pi }{2}} \right) = 30\cos \left( {5\pi t} \right)(cm/s)\)
b) Từ đồ thị ta có :
Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
\( = > x = \frac{6}{\pi }\cos \left( {5\pi t - \frac{\pi }{2}} \right)(cm)\)
Phương trình của gia tốc có dạng : \(a = A{\omega ^2}\cos \left( {\omega t + \varphi + \pi } \right)\)
\( = > a = 150\pi \cos \left( {5\pi t + \frac{\pi }{2}} \right)(cm/{s^2})\)
