Câu hỏi/bài tập:
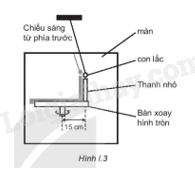
Hình I.3 là sơ đồ của một bàn xoay hình tròn, có gắn một thanh nhỏ cách tâm bàn 15 cm. Bàn xoay được chiều sáng từ bên cạnh phía trước màn để bóng đổ lên màn hình. Một con lắc đơn được đặt sau bàn xoay và làm cho dao động điều hoà với biên độ bằng khoảng cách từ thanh nhỏ đền tâm bàn xoay. Tốc độ quay của bàn quay được điều chỉnh là \(2\pi \) rad/s và bóng của thanh nhỏ luôn trùng với bóng của con lắc trên màn hình.
a) Tại sao nói dao động của bóng của thanh nhỏ và quả lắc là đồng pha ?
b) Viết phương trình mô tả li độ x của con lắc khỏi vị trí cân. Chọn gốc
thời gian là lúc con lắc ở vị trí hiển thị trong sơ đồ.
c) Bàn xoay đi một góc \({60^0}\) từ vị trí ban đầu. Tính li độ của con lắc và tốc độ
của nó tại thời điểm này. Bàn xoay phải quay thêm một góc nào nữa
trước khi nó có tốc độ này trở lại?

Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với:
+ \(x\) là li độ dao động.
Advertisements (Quảng cáo)
+ \(A\) là biên độ dao động.
+ \(\omega \) là tần số góc của dao động.
+ \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t.
+\(\varphi \) là pha ban đầu.
Lời giải chi tiết :
a) Dao động của bóng của thanh nhỏ và quả nặng đồng pha với nhau vì chúng luôn xuất hiện cùng lúc .
b) Biên độ dao động của con lắc A= 15 cm
Tần số góc \(\omega = 2\pi (rad/s)\). Từ hình vẽ và hướng di chuyển của con lắc ta có pha ban đầu \(\varphi = 0\)
Phương trình dao động của con lắc là : \(x = 15\cos 2\pi t\left( {cm} \right)\)
c) Bàn xoay đi một góc \({60^o}\)từ vị trí ban đầu ta có pha dao động của con lắc là \(\frac{\pi }{3}\)
Li độ của con lắc là \(x = 7,5cm\)
Vận tốc của con lắc là \(v = \left| { \pm \omega \sqrt {{A^2} - {x^2}} } \right| = 15\sqrt 3 \pi (cm/s)\)
