Câu hỏi/bài tập:
Cho mạch điện như Hình IV.1. Biết giá trị cáo điện trở:\({R_1} = 4\Omega \), \({R_2} = 6\Omega \), \({R_3} = 12\Omega \). Hiệu điện thế giữa hai đầu đoạn mạch \({U_{AD}}\)= 6V. Giả sử điện trở của dây nối và của ampe kế không đáng kể. Tính số chỉ của ampe kế khi:
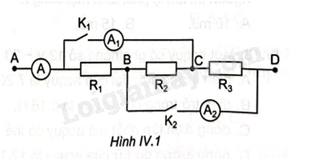
a)\({K_1}\) ngắt, \({K_2}\)đóng.
b) \({K_1}\)đóng, \({K_2}\) ngắt.
c) \({K_1}\),\({K_2}\)đều ngắt,
d) \({K_1}\), \({K_2}\) đều đóng.

Định luật Ohm trong các đoạn mạch.

a)\({K_1}\) ngắt, \({K_2}\)đóng.
B với D nối với nhau bằng dây nối => chập B lại với điểm D dòng ưu tiên qua dây nối không qua \({R_2};{R_3}\)=> có thể bỏ qua \({R_2};{R_3}\)=> mạch chỉ còn \({R_1}\)
=> Số chỉ ampe kế : \(I = \frac{{{U_{AD}}}}{{{R_1}}} = \frac{6}{4} = 1,5A\)
b) \({K_1}\)đóng, \({K_2}\) ngắt.
A với C nối với nhau bằng dây nối => chập A lại với điểm C dòng ưu tiên qua dây nối không qua \({R_1};{R_2}\)=> có thể bỏ qua \({R_1};{R_2}\)=> mạch chỉ còn \({R_3}\)
=> Số chỉ ampe kế : \(I = \frac{{{U_{AD}}}}{{{R_3}}} = \frac{6}{{12}} = 0,5A\)
Advertisements (Quảng cáo)
c) \({K_1}\),\({K_2}\)đều ngắt
Mạch mới
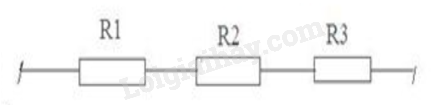
Mạch nối tiếp nên cường độ dòng điện bằng nhau => Số chỉ ampe kế :
\(I = \frac{{{U_{AD}}}}{{{R_N}}} = \frac{{{U_{AD}}}}{{{R_1} + {R_2} + {R_3}}} = \frac{6}{{4 + 6 + 12}} = \frac{3}{{11}}A\)
d) \({K_1}\), \({K_2}\) đều đóng.
Vì ampe kế có điện trở không đáng kể nên:
+ A và C có cùng điện thế → chập C và A lại.
+ B và D có cùng điện thế → chập D và B lại.
Mạch điện được vẽ lại như sau:
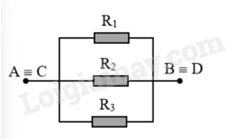
Ta có : \({R_1}//{R_2}//{R_3} = > \frac{1}{{{R_{AB}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}} = \frac{1}{4} + \frac{1}{6} + \frac{1}{{12}} = > {R_{AB}} = 0,5A\)
=> Số chỉ ampe kế \( = > {I_A} = \frac{U}{{{R_{AB}}}} = \frac{6}{{0,5}} = 12A\);
\({I_1} = \frac{U}{{{R_1}}} = \frac{6}{4} = 1,5A\); \({I_3} = \frac{U}{{{R_3}}} = \frac{6}{{12}} = 0,5A\)
=> Số chỉ ampe kế 1 : \({I_A} = {I_1} + {I_{A1}} = > {I_{A1}} = {I_A} - {I_1} = 12 - 1,5 = 10,5A\)
=> Số chỉ ampe kế 2 : \({I_A} = {I_3} + {I_{A2}} = > {I_{A2}} = {I_A} - {I_3} = 12 - 0,5 = 11,5A\)
