Bài 7. Bài tập về sự chuyển hóa năng lượng trong dao động điều hòa trang 28, 29, 30 Vật lý 11 Kết nối tri thức: Ta có thể sử dụng định luật bảo toàn cơ năng để tìm li độ và...

Câu hỏi trang 28 Khởi động

Ta có thể sử dụng định luật bảo toàn cơ năng để tìm li độ và vận tốc của vật dao động điều hòa được không?

Dựa vào nội dung kiến thức đã học về cơ năng để trả lời.

Với định luật bảo toàn cơ năng ta có thể tìm được li độ và vận tốc vật trong dao động điều hòa

W_đ + W_t = W ⇔\(\frac{1}{2}m{v^2} + \frac{1}{2}m{\omega ^2}{x^2} = \frac{1}{2}m{\omega ^2}{A^2}\)

Bài tập luyện tập Bài 1

Hình 7.3 mô tả một máy đo địa chấn đơn giản hoạt động theo nguyên tắc sau đây: Khi xảy ra động đất thì hệ gồm lò xo và vật nặng của máy đo sẽ dao động theo tần số của địa chấn. Bút dạ gắn với vật nặng sẽ ghi lại đồ thị của địa chấn trên cuộn giấy quay đều. Biết sóng địa chấn có tần số nằm trong khoảng từ 30 Hz đến 40 Hz.

Hãy giải thích tại sao tần số riêng của hệ (vật nặng + lò xo) trong máy địa chấn phải có giá trị nhỏ hơn tần số nay rất nhiều.

Dựa vào nội dung kiến thức đã học để trả lời.

Tần số riêng của hệ (vật nặng + lò xo) trong máy địa chấn phải có giá trị nhỏ hơn tần số sóng địa chấn vì để tránh xảy ra hiện tượng cộng hưởng dao động gây hỏng máy không đo được tần số dao động.

Bài tập luyện tập Bài 2

Đồ thị Hình 7.4 mô tả mối liên hệ giữa gia tốc và li độ của một vật dao động điều hoà. Sử dụng số liệu trong đồ thị Hình 7.4 để tính tần số của dao động

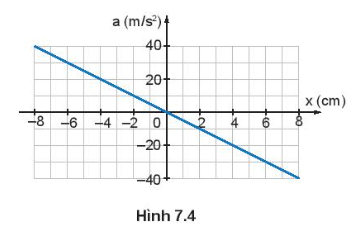
Dựa vào nội dung kiến thức đã học và công thức của dao động điều hòa để trả lời.

Ta có: x = -0,04 (m) thì a = 20 (m/s²)

\( \Rightarrow a = - {\omega ^2}x \Leftrightarrow a = - {\left( {2\pi f} \right)^2}x \Leftrightarrow 20 = {\left( {2\pi f} \right)^2}.0,04 \Leftrightarrow f = \frac{{5\sqrt 5 }}{{\pi }}(Hz)\)

Bài tập luyện tập Bài 3

Hình 7.5 là đồ thị động năng theo thời gian của một vật khối lượng 0,4 kg dao động điều hoà. Tại thời điểm ban đầu vật đang chuyển động theo chiều dương, lấy π² = 10. Viết phương trình dao động của vật.

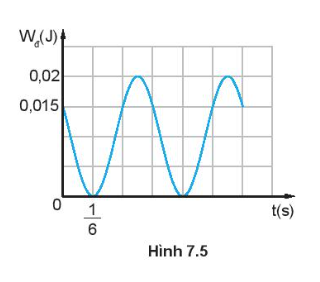
Dựa vào nội dung kiến thức đã học và công thức của dao động điều hòa để trả lời.

Từ đồ thị ta có:

Tại thời điểm ban đầu t = 0: W_đ = 0,015 J ⇒W_t = 0,02−0,015 = 0,005(J)

⇔\({{\rm{W}}_t} = \frac{{\rm{W}}}{4} \Rightarrow {x_0} = \pm \frac{A}{2}\)

Tại thời điểm t₁ = \(\frac{1}{6}\): W_đ = 0 ⇒ x₁ = ±A

Dựa vào đồ thị ta suy ra: x₀ = \(\frac{A}{2}\); x₁ = A

Khoảng thời gian từ x₀ đến x₁ là: Δt = \(\frac{T}{6}\)⇔T = 1(s) ⇔ ω = \(\frac{{2\pi }}{T} = 2\pi \) (rad/s)

\({{\rm{W}}_{{\rm{dmax}}}} = \frac{1}{2}m{\omega ^2}{A^2} = 0,02 \Leftrightarrow A = \sqrt {\frac{{{{\rm{W}}_{{\rm{dmax}}}}}}{{m{\omega ^2}}}} = \sqrt {\frac{{2.0,02}}{{0,4{{\left( {2\pi } \right)}^2}}}} = 0,05m = 5cm\)

Tại t=0:

\(\left\{ \begin{array}{c}{x_0} = A\cos \varphi = \frac{A}{2}\\v = - A\sin \varphi > 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\cos \varphi = \frac{1}{2}\\\sin \varphi < 0\end{array} \right. \Rightarrow \varphi = - \frac{\pi }{3}\)

Phương trình dao động của vật: x = 5cos(2πt − \(\frac{\pi }{3}\))(cm)

Bài tập luyện tập Bài 4

Một vật có khối lượng m dao động điều hoà với tần số góc ở và biên độ A.

a) Khi vật có li độ bằng một nửa biên độ thì động năng và thế năng chiếm bao nhiêu phần trăm so với cơ năng?

b) Tại li độ nào thì thế năng bằng động năng?

Dựa vào nội dung kiến thức đã học và công thức của dao động điều hòa để trả lời.

a) Ta có:

\(x = \frac{A}{2} \Rightarrow \frac{{{{\rm{W}}_t}}}{{\rm{W}}} = \frac{{\frac{1}{2}m{\omega ^2}{x^2}}}{{\frac{1}{2}m{\omega ^2}{A^2}}} = \frac{1}{4} \Rightarrow {{\rm{W}}_t} = 25\% {\rm{W}};{{\rm{W}}_d} = 75\% {\rm{W}}\)

b) Ta có: W_t = W_đ ⇒\(\frac{{{{\rm{W}}_t}}}{{\rm{W}}} = \frac{{\frac{1}{2}m{\omega ^2}{x^2}}}{{\frac{1}{2}m{\omega ^2}{A^2}}} = \frac{1}{2} \Rightarrow x = \frac{A}{{\sqrt 2 }}\)