Câu hỏi trang 54 Câu hỏiMở đầu (MĐ)
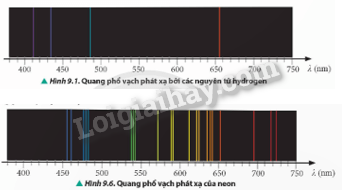
Vào đầu thế kỉ XX, các nhà vật lý đã khám phá ra một số hiện tượng mà vật lý cổ điển không thể giải thích một cách thỏa đáng như hiện tượng các chất khí (hydrogen và các ion tương tự) khi hấp thụ năng lượng sẽ phát ra quang phổ vạch gồm các vạch màu riêng lẻ (Hình 9.1). Ngoài ra, mô hình hành tinh nguyên tử của Rutherford cũng không thể giải thích được vì sao các electron mang điện tích âm chuyển động tròn quanh hạt nhân mang điện tích dương lại không mất năng lượng và rơi vào trong hạt nhân. Mô hình nguyên tử do nhà vật lý người Đan Mạch Niels Bohr (Nây Bo) (Hình 9.2) đề xuất đã giải quyết được những vấn đề trên



Tìm hiểu qua sách báo, internet

Mô hình nguyên tử của Bohr
Câu hỏi trang 55 Câu hỏi
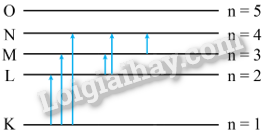
Sử dụng sơ đồ ở Hình 9.3, tính năng lượng cần thiết để nguyên tử hydrogen chuyển từ trạng thái cơ bản đến trạng thái có năng lượng bằng 0 (năng lượng ion hoá nguyên tử).


Vận dụng kiến thức về mức năng lượng

Năng lượng cần thiết để nguyên tử hydrogen chuyển từ trạng thái cơ bản đến trạng thái có năng lượng bằng không (năng lượng ion hoá nguyên tử):
\(\varepsilon = {E_\infty } - {E_1} = 0 - \left( { - 13,6} \right) = 13,6\,eV\)
Câu hỏi trang 56 Luyện tập (LT)
Quan sát các mức năng lượng của nguyên tử hydrogen ở Hình 9.3 và cho biết nếu cung cấp một năng lượng bằng 12,09 eV cho nguyên tử hydrogen đang ở trạng thái cơ bản thì nguyên tử này sẽ chuyển lên trạng thái kích thích tương ứng với mức năng lượng nào. Sau đó, nguyên tử hydrogen có thể phát xạ các photon có bước sóng bằng bao nhiêu?

Vận dụng kiến thức về mức năng lượng

Ta có: \(\varepsilon = {E_n} - {E_m} \Rightarrow {E_n} = \varepsilon + {E_m} = 12,09 - 13,6 = - 1,51{\rm{\;eV}}\)
mà \({E_n} = \frac{{ - 13,6}}{{{n^2}}} = - 1,51 \Rightarrow n \approx 3\). Khi đó nguyên tử sẽ ở mức M.
\(\varepsilon = \frac{{hc}}{\lambda } \Rightarrow \frac{{{{12,09.1,6.10}^{ - 19}}}}{\lambda } = \frac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{\lambda } \Rightarrow \lambda = {10^{ - 7}}{\rm{\;m}}\)
Câu hỏi trang 57 Câu hỏi 1
Quan sát Hình 9.1 và 9.6, so sánh quang phổ vạch phát xạ của nguyên tử hydrogen và neon về số lượng vạch.

Vận dụng kiến thức về quang phổ vạch

- Quang phổ vạch phát xạ của nguyên tử hydrogen: gồm một số vạch sáng, đơn lẻ, tập trung chủ yếu ở vùng ánh sáng nhìn thấy. Các vạch có màu sắc đặc trưng như: đỏ, lam, tím,…
- Quang phổ vạch phát xạ của nguyên tử neon: gồm nhiều vạch sáng, phức tạp hơn so với hydrogen. Các vạch trải dài trên toàn bộ vùng ánh sáng nhìn thấy từ đỏ đến tím.
Số lượng vạch của quang phổ vạch phát xạ của neon lớn hơn nhiều so với của hydrogen.
Câu hỏi trang 57 Câu hỏi 2
So sánh số vạch và vị trí của các vạch phổ phát xạ (Hình 9.7a) và các vạch phổ hấp thụ (Hình 9.7b) của nguyên tử hydrogen.


Vận dụng kiến thức về quang phổ vạch

Advertisements (Quảng cáo)
- Quang phổ phát xạ:
+ Gồm một số vạch sáng, đơn lẻ, trên nền tối.
+ Trùng khớp với vị trí các vạch tối trong quang phổ hấp thụ.
- Quang phổ hấp thụ:
+ Gồm nhiều vạch tối trên nền quang phổ liên tục.
+ Trùng khớp với vị trí các vạch sáng trong quang phổ phát xạ.
Câu hỏi trang 58 Luyện tập (LT)
So sánh quang phổ vạch phát xạ và quang phổ vạch hấp thụ của mỗi chất khí.

Vận dụng kiến thức về quang phổ vạch

Giống nhau: Vị trí các vạch sáng trong quang phổ vạch phát xạ trùng với vị trí các vạch tối trong quang phổ vạch hấp thụ.
- Khác nhau:
+ Quang phổ vạch phát xạ: số lượng vạch ít, vạch sáng, rõ nét.
+ Quang phổ vạch hấp thụ: số lượng vạch nhiều, vạch tối có thể mờ hoặc đậm.
Câu hỏi trang 58 Vận dụng (VD)
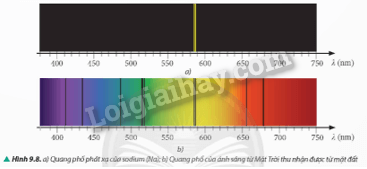
Quan sát quang phổ vạch phát xạ của nguyên tử hydrogen (H) (Hình 9.7a), quang phổ vạch phát xạ của nguyên tử sodium (Na) (Hình 9.8a) và quang phổ của ánh sáng mặt trời thu nhận được từ mặt đất (Hình 9.8b). Giải thích sự xuất hiện các vạch tối trên nền màu liên tục trong Hình 9.8b. Vì sao từ các vạch tối này, ta có thể khẳng định trong khí quyển quanh Trái Đất có tồn tại nguyên tử hydrogen (H) và nguyên tử sodium (Na).

Vận dụng kiến thức về quang phổ vạch

Sự xuất hiện các vạch tối trên nền màu liên tục trong Hình 9.8b vì: Vạch tối xuất hiện do hiện tượng hấp thụ ánh sáng. Ánh sáng từ Mặt Trời (gồm nhiều bước sóng khác nhau) đi qua khí quyển Trái Đất. Các nguyên tử hydrogen và sodium trong khí quyển hấp thụ một phần ánh sáng với các bước sóng nhất định tương ứng với các mức năng lượng của chúng khiến các bước sóng đó không thể đến được Trái Đất, tạo nên các vạch tối trên nền màu liên tục.
Các vạch tối này, ta có thể khẳng định trong khí quyển quanh Trái Đất có tồn tại nguyên tử hydrogen (H) và nguyên tử sodium (Na) vì:
Dựa trên vạch D: Vạch D màu vàng trong quang phổ ánh sáng mặt trời cho thấy sự tồn tại của nguyên tử sodium trong khí quyển Trái Đất.
Dựa trên các vạch tối khác: So sánh vị trí các vạch tối trong quang phổ ánh sáng mặt trời với vị trí các vạch sáng trong quang phổ phát xạ của hydrogen. Nếu trùng khớp, khẳng định sự tồn tại của nguyên tử hydrogen trong khí quyển Trái Đất
Bài tập Bài 1
Sử dụng các giá trị của các mức năng lượng của nguyên tử hydrogen trong Hình 9.3 để tính các bước sóng do nguyên tử này phát xạ khi thực hiện các chuyển dời từ các mức năng lượng E3, E4, E5 và E6 về mức năng lượng E2.

Vận dụng kiến thức về mức năng lượng

\(\begin{array}{l}{E_{32}} = {E_3} - {E_2} = - \frac{{13,6}}{{{3^2}}} - \left( { - \frac{{13,6}}{{{2^2}}}} \right) = 1,89\,eV\\{E_{42}} = {E_4} - {E_2} = - \frac{{13,6}}{{{4^2}}} - \left( { - \frac{{13,6}}{{{2^2}}}} \right) = 2,55\,eV\\{E_{52}} = {E_5} - {E_2} = - \frac{{13,6}}{{{5^2}}} - \left( { - \frac{{13,6}}{{{2^2}}}} \right) = 2,89\,eV\\{E_{62}} = {E_6} - {E_2} = - \frac{{13,6}}{{{6^2}}} - \left( { - \frac{{13,6}}{{{2^2}}}} \right) = 3,02\,eV\end{array}\)
Bài tập Bài 2
Để nguyên tử hydrogen đang ở trạng thái cơ bản có thể phát xạ được sáu vạch quang phổ, cần phải cung cấp năng lượng để nguyên tử này chuyển dời lên mức kích thích nào? Vẽ sơ đồ dịch chuyển giữa các mức năng lượng.

Vận dụng kiến thức về mức năng lượng

Số vạch quang phổ tối đa: \(C_n^2 = \frac{{n\left( {n - 1} \right)}}{2} = 6 \Rightarrow n = 4\)
Vậy nguyên tử chuyển dời lên mức n = 4 (N)