
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).
Cho mẫu số liệu ghép nhóm như Bảng 19.
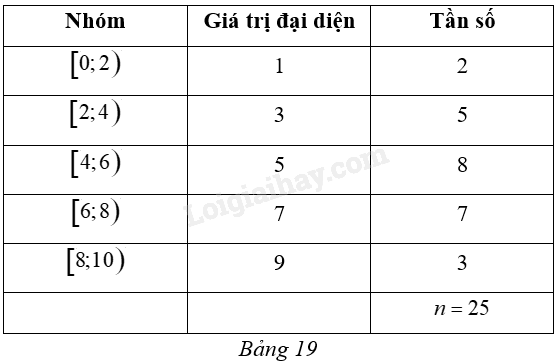
a) Khoảng biến thiên của mẫu số liệu ghép nhóm là 2.
b) Số trung bình của mẫu số liệu ghép nhóm là 5,32.
c) Phương sai của mẫu số liệu ghép nhóm là 5,0176.
d) Độ lệch chuẩn của mẫu số liệu ghép nhóm là 2,24.

‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} - {a_1}\).
‒ Sử dụng công thức tính số trung bình cộng của mẫu số liệu ghép nhóm: \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\)trong đó \(n = {m_1} + ... + {m_k}\) là cỡ mẫu và \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) (với \(i = 1,...,k\)) là giá trị đại diện của nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\).
‒ Sử dụng công thức tính phương sai của mẫu số liệu ghép nhóm:
\({s^2} = \frac{{{n_1}{{\left( {{x_1} - \overline x } \right)}^2} + {n_2}{{\left( {{x_2} - \overline x } \right)}^2} + ... + {n_m}{{\left( {{x_m} - \overline x } \right)}^2}}}{n}\)
Advertisements (Quảng cáo)
‒ Sử dụng công thức tính độ lệch chuẩn của mẫu số liệu ghép nhóm: \(s = \sqrt {{s^2}} \).

Khoảng biến thiên của mẫu số liệu ghép nhóm là: \(R = 10 - 0 = 10\). Vậy a) sai.
Số trung bình cộng của mẫu số liệu ghép nhóm là: \(\overline x = \frac{{2.1 + 5.3 + 8.5 + 7.7 + 3.9}}{{25}} = 5,32\)
Vậy b) đúng.
Phương sai của mẫu số liệu ghép nhóm đó là:
\(\begin{array}{l}{s^2} = \frac{1}{{25}}\left[ {2.{{\left( {1 - 5,32} \right)}^2} + 5.{{\left( {3 - 5,32} \right)}^2} + 8.{{\left( {5 - 5,32} \right)}^2} + 7.{{\left( {7 - 5,32} \right)}^2} + 3.{{\left( {9 - 5,32} \right)}^2}} \right]\\ = \frac{{3135}}{{625}} = 5,0176\end{array}\)
Vậy c) đúng.
Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \(s = \sqrt {5,0176} \approx 2,24\). Vậy d) đúng.
a) S.
b) Đ.
c) Đ.
d) Đ.
