
Bảng 22 thống kê độ ẩm không khí trung bình các tháng năm 2022 tại Đà Nẵng và Quy Nhơn (đơn vị: %).

a) Hãy lần lượt ghép các số liệu của Đà Nẵng, Quy Nhơn thành năm nhóm sau: \(\left[ {71;74} \right),\)\(\left[ {74;77} \right),\left[ {77;80} \right),\left[ {80;83} \right),\left[ {83;86} \right)\).
b) Tính khoảng biến thiên, khoảng tứ phân vị, phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm của Đà Nẵng và Quy Nhơn.

‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} - {a_1}\).
‒ Sử dụng công thức tính các tứ phân vị của mẫu số liệu ghép nhóm:
+ Nhóm thứ \(p\) là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{4}\) (tức là \(c{f_{p - 1}}
+ Nhóm thứ \(q\) là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{{3n}}{4}\) (tức là \(c{f_{q - 1}}
‒ Sử dụng công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm: \(\Delta Q = {Q_3} - {Q_1}\).
‒ Sử dụng công thức tính số trung bình cộng của mẫu số liệu ghép nhóm: \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\)trong đó \(n = {m_1} + ... + {m_k}\) là cỡ mẫu và \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) (với \(i = 1,...,k\)) là giá trị đại diện của nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\).
‒ Sử dụng công thức tính phương sai của mẫu số liệu ghép nhóm:
\({s^2} = \frac{{{n_1}{{\left( {{x_1} - \overline x } \right)}^2} + {n_2}{{\left( {{x_2} - \overline x } \right)}^2} + ... + {n_m}{{\left( {{x_m} - \overline x } \right)}^2}}}{n}\)
‒ Sử dụng công thức tính độ lệch chuẩn của mẫu số liệu ghép nhóm: \(s = \sqrt {{s^2}} \).

a) Ta có bảng sau:
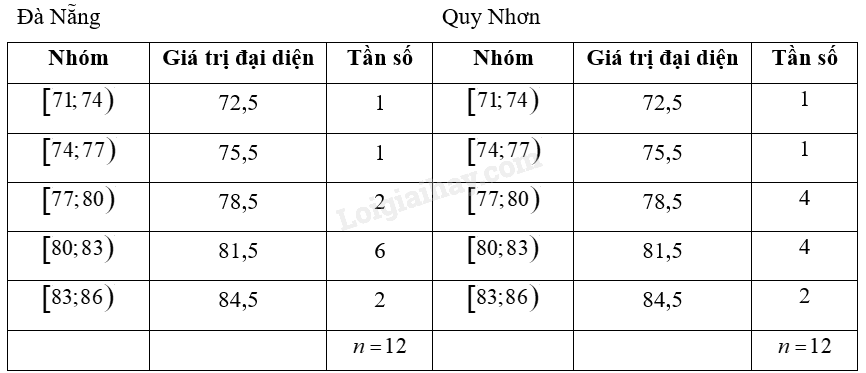
b) • Đà Nẵng:
Khoảng biến thiên của mẫu số liệu ghép nhóm là: \(R = 86 - 71 = 15\).
Nhóm 3 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{4} = \frac{{12}}{4} = 3\).
Nhóm 3 có đầu mút trái \(s = 77\), độ dài \(h = 3\), tần số của nhóm \({n_3} = 2\) và nhóm 2 có tần số tích luỹ \(c{f_2} = 1 + 1 = 2\).
Ta có: \({Q_1} = s + \left( {\frac{{3 - c{f_2}}}{{{n_3}}}} \right).h = 77 + \left( {\frac{{3 - 2}}{2}} \right).3 = 78,5\) (%).
Advertisements (Quảng cáo)
Nhóm 4 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{{3n}}{4} = \frac{{3.12}}{4} = 9\).
Nhóm 4 có đầu mút trái \(t = 80\), độ dài \(l = 3\), tần số của nhóm \({n_4} = 6\) và nhóm 3 có tần số tích luỹ \(c{f_3} = 1 + 1 + 2 = 4\).
Ta có: \({Q_3} = t + \left( {\frac{{9 - c{f_3}}}{{{n_4}}}} \right).l = 80 + \left( {\frac{{9 - 4}}{6}} \right).3 = 82,5\) (%).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \(\Delta Q = {Q_3} - {Q_1} = 82,5 - 78,5 = 4\) (%).
Số trung bình cộng của mẫu số liệu ghép nhóm là:
\(\overline x = \frac{{1.72,5 + 1.75,5 + 2.78,5 + 6.81,5 + 2.84,5}}{{12}} = 80,25\)
Phương sai của mẫu số liệu ghép nhóm đó là:
\(\begin{array}{l}{s^2} = \frac{1}{{12}}\left[ {1.{{\left( {72,5 - 80,25} \right)}^2} + 1.{{\left( {75,5 - 80,25} \right)}^2} + 2.{{\left( {78,5 - 80,25} \right)}^2} + 6.{{\left( {81,5 - 80,25} \right)}^2} + } \right.\\\left. { + 2.{{\left( {84,5 - 80,25} \right)}^2}} \right] = 11,1875\end{array}\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \(s = \sqrt {11,1875} \approx 3,3448\).
• Quy Nhơn:
Khoảng biến thiên của mẫu số liệu ghép nhóm là: \(R = 86 - 71 = 15\).
Nhóm 3 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{4} = \frac{{12}}{4} = 3\).
Nhóm 3 có đầu mút trái \(s = 77\), độ dài \(h = 3\), tần số của nhóm \({n_3} = 4\) và nhóm 2 có tần số tích luỹ \(c{f_2} = 1 + 1 = 2\).
Ta có: \({Q_1} = s + \left( {\frac{{3 - c{f_2}}}{{{n_3}}}} \right).h = 77 + \left( {\frac{{3 - 2}}{4}} \right).3 = 77,75\) (%).
Nhóm 4 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{{3n}}{4} = \frac{{3.12}}{4} = 9\).
Nhóm 4 có đầu mút trái \(t = 80\), độ dài \(l = 3\), tần số của nhóm \({n_4} = 4\) và nhóm 3 có tần số tích luỹ \(c{f_3} = 1 + 1 + 4 = 6\).
Ta có: \({Q_3} = t + \left( {\frac{{9 - c{f_3}}}{{{n_4}}}} \right).l = 80 + \left( {\frac{{9 - 6}}{4}} \right).3 = 82,25\) (%).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \(\Delta Q = {Q_3} - {Q_1} = 82,25 - 77,75 = 4,5\) (%).
Số trung bình cộng của mẫu số liệu ghép nhóm là:
\(\overline x = \frac{{1.72,5 + 1.75,5 + 4.78,5 + 4.81,5 + 2.84,5}}{{12}} = 79,75\)
Phương sai của mẫu số liệu ghép nhóm đó là:
\(\begin{array}{l}{s^2} = \frac{1}{{12}}\left[ {1.{{\left( {72,5 - 79,75} \right)}^2} + 1.{{\left( {75,5 - 79,75} \right)}^2} + 4.{{\left( {78,5 - 79,75} \right)}^2} + 4.{{\left( {81,5 - 79,75} \right)}^2} + } \right.\\\left. { + 2.{{\left( {84,5 - 79,75} \right)}^2}} \right] = 11,1875\end{array}\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \(s = \sqrt {11,1875} \approx 3,3448\).
