
Biểu đồ tần số tương đối ghép nhóm sau cho biết phân bố về khối lượng của 200 bao xi măng trước khi xuất xưởng:
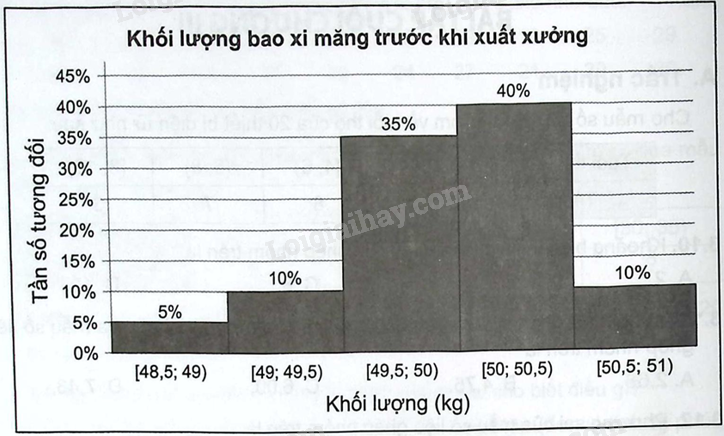
a) Lập bảng tần số ghép nhóm cho dữ liệu về khối lượng của 200 bao xi măng trên.
b) Tính khoảng tứ phân vị cho mẫu số liệu ghép nhóm thu được ở câu a.

Ý a: Lập bảng có 2 hàng, hàng thứ nhất là khối lượng, hàng thứ hai là số bao xi măng. Dữ liệu có trong mỗi ô được xác định từ biểu đồ trong đề bài.
Ý b: Thực hiện từng bước, tìm vị trí, tính \({Q_1}\), \({Q_3}\) sau đó tính khoảng tứ phân vị bằng công thức đã học.
Advertisements (Quảng cáo)

a) Từ biểu đồ, ta lập bảng tần số ghép nhóm cho dữ liệu về khối lượng của 200 bao xi măng như sau ( với tần số-số bao xi măng được bằng tổng số bao xi măng là 200 nhân với tỉ lệ phần trăm tương ứng của từng cột trên biểu đồ):

b) Cỡ mẫu là \(n = 200\).
Vị trí của \({Q_1}\) là \(\frac{n}{4} = 50\) suy ra nhóm chứa tứ phân vị thứ nhất là \(\left[ {49,5;50} \right)\).
Ta có \({Q_1} = 49,5 + \frac{{\frac{{1 \cdot 200}}{4} - 30}}{{70}} \cdot 0,5 = \frac{{695}}{{14}}\).
Tương tự có vị trí của \({Q_3}\) là \(\frac{{3n}}{4} = 150\) suy ra nhóm chứa tứ phân vị thứ ba là \(\left[ {50;50,5} \right)\). Do đó \({Q_3} = 50 + \frac{{\frac{{3 \cdot 200}}{4} - 100}}{{80}} \cdot 0,5 = 50,3125\).
Suy ra khoảng tứ phân vị là \({\Delta _Q} = {Q_3} - {Q_1} = 50,3125 - \frac{{695}}{{14}} \approx 0,6696\).
