
Một công ty giống cây trồng đã thử nghiệm hai phương pháp chăm sóc khác nhau cho cây hướng dương. Sau hai tuần, người ta thấy cây được chăm sóc theo cả hai phương pháp đều thấp hơn 50 cm. Hình 3.5a và 3.5b biểu diễn chiều cao của một số cây.
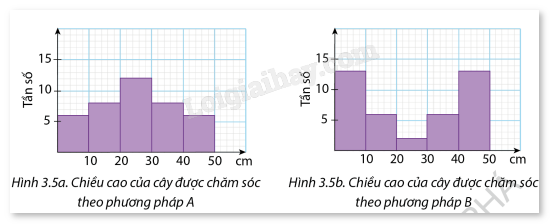
a) Ước tính số trung bình và độ lệch chuẩn của chiều cao các cây được chăm sóc theo mỗi phương pháp.
b) So sánh hiệu quả của các phương pháp trên hai phương diện:
- Chiều cao trung bình của cây.
- Sự đồng đều về chiều cao của cây.

a) Áp dụng các công thức sau:
- Công thức tính trung bình:
\(\bar x = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{f_i}} \right)} }}{N}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {\overline {{x^2}} - {{\left( {\bar x} \right)}^2}} = \sqrt {\frac{{\sum {{f_i}x_i^2} }}{N} - {{\left( {\bar x} \right)}^2}} \)
b)
- So sánh giá trị trung bình của hai phương pháp để đánh giá chiều cao trung bình của cây.
- So sánh độ lệch chuẩn của hai phương pháp để đánh giá sự đồng đều về chiều cao của cây.

a) Bảng phân phối tần số cho phương pháp A và B:
Advertisements (Quảng cáo)
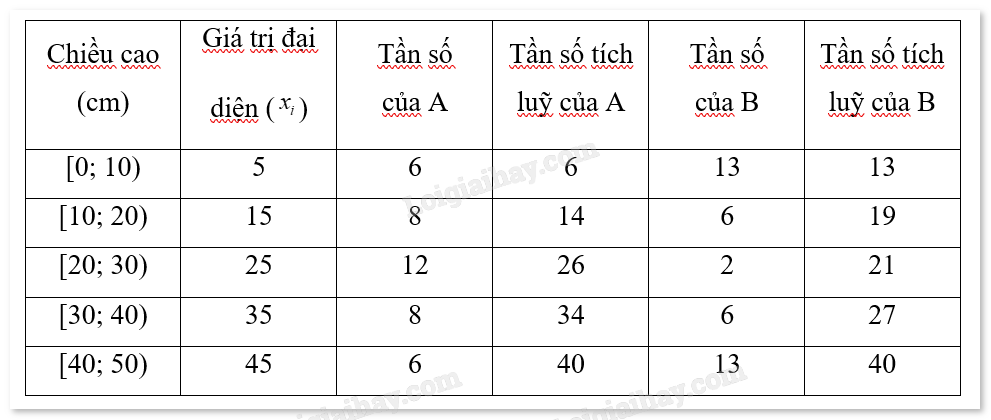
Dựa vào bảng phân phối ta thấy N = 40
Giá trị trung bình của phương pháp A:
\({\bar x_A} = \frac{1}{N}\sum\limits_{i = 1}^k {{f_i}} \times {x_i} = \frac{{6 \times 5 + 8 \times 15 + 12 \times 25 + 8 \times 35 + 6 \times 45}}{{40}} = 25cm\)
Độ lệch chuẩn của phương pháp A:
\({S_A} = \sqrt {\frac{1}{{40}}\sum\limits_{i = 1}^5 {{f_i}} \times {{({x_i} - 25)}^2}} \)
\({S_A} = \sqrt {\frac{{6 \times {{(5 - 25)}^2} + 8 \times {{(15 - 25)}^2} + 12 \times {{(25 - 25)}^2} + 8 \times {{(35 - 25)}^2} + 6 \times {{(45 - 25)}^2}}}{{40}}} \)
\({S_A} = \sqrt {160} = 4\sqrt {10} \approx 12,65cm\)
Giá trị trung bình của phương pháp B:
\({\bar x_B} = \frac{1}{N}\sum\limits_{i = 1}^k {{f_i}} \times {x_i} = \frac{{13 \times 5 + 6 \times 15 + 2 \times 25 + 6 \times 35 + 13 \times 45}}{{40}} = 25cm\)
Độ lệch chuẩn của phương pháp B:
\({S_B} = \sqrt {\frac{1}{{40}}\sum\limits_{i = 1}^5 {{f_i}} \times {{({x_i} - 25)}^2}} \)
\({S_B} = \sqrt {\frac{{13 \times {{(5 - 25)}^2} + 6 \times {{(15 - 25)}^2} + 2 \times {{(25 - 25)}^2} + 6 \times {{(35 - 25)}^2} + 13 \times {{(45 - 25)}^2}}}{{40}}} \)
\({S_B} = \sqrt {290} \approx 17,03cm\)
b)
- Chiều cao trung bình: Cả hai phương pháp có cùng số trung bình là 25 cm, cho thấy rằng chiều cao trung bình của các cây là như nhau trong cả hai phương pháp chăm sóc.
- Sự đồng đều về chiều cao của cây: Phương pháp A có độ lệch chuẩn nhỏ hơn (12.65 cm) so với phương pháp B (17.03 cm), chỉ ra rằng cây trong phương pháp A có sự đồng đều về chiều cao hơn so với cây trong phương pháp B.
