Câu 1
Trả lời câu hỏi 1 trang 30
Tính
a) $\frac{9}{8} + \frac{4}{5}$
b) \(\frac{6}{5} - \frac{5}{{14}}\)
c) $\frac{2}{9} + \frac{1}{6}$
d) \(\frac{5}{6} - \frac{3}{4}\)

Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số đó, rồi cộng (hoặc trừ) hai phân số đã quy đồng.

a) $\frac{9}{8} + \frac{4}{5} = \frac{{45}}{{40}} + \frac{{32}}{{40}} = \frac{{77}}{{40}}$
b) \(\frac{6}{5} - \frac{5}{{14}} = \frac{{84}}{{70}} - \frac{{25}}{{70}} = \frac{{59}}{{70}}\)
c) $\frac{2}{9} + \frac{1}{6} = \frac{4}{{18}} + \frac{3}{{18}} = \frac{7}{{18}}$
d) \(\frac{5}{6} - \frac{3}{4} = \frac{{10}}{{12}} - \frac{9}{{12}} = \frac{1}{{12}}\)
Câu 2
Trả lời câu hỏi 2 trang 30
Chọn giá trị đúng cho mỗi biểu thức
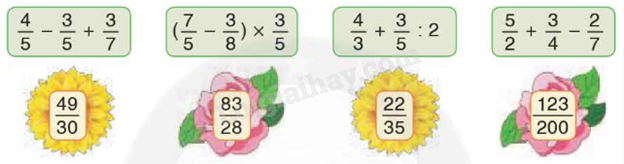

Thứ tự thực hiện phép tính:
- Khi thực hiện các phép tính trong biểu thức, ta thực hiện từ trái qua phải.
- Nếu biểu thức có dấu ngoặc, ta thực hiện các phép toán trong ngoặc trước.
- Nếu biểu thức gồm các phép tính cộng, trừ, nhân, chia thì ta thực hiện phép toán nhân, chia trước sau đó mới đến phép toán cộng, trừ.

Ta có:
\(\frac{4}{5} - \frac{3}{5} + \frac{3}{7} = \frac{1}{5} + \frac{3}{7} = \frac{7}{{35}} + \frac{{15}}{{35}} = \frac{{22}}{{35}}\)
\(\left( {\frac{7}{5} - \frac{3}{8}} \right) \times \frac{3}{5} = \left( {\frac{{56}}{{40}} - \frac{{15}}{{40}}} \right) \times \frac{3}{5} = \frac{{41}}{{40}} \times \frac{3}{5} = \frac{{123}}{{200}}\)
\(\frac{4}{3} + \frac{3}{5}:2 = \frac{4}{3} + \frac{3}{5} \times \frac{1}{2} = \frac{4}{3} + \frac{3}{{10}} = \frac{{40}}{{30}} + \frac{9}{{30}} = \frac{{49}}{{30}}\)
\(\frac{5}{2} + \frac{3}{4} - \frac{2}{7} = \frac{{70}}{{28}} + \frac{{21}}{{28}} - \frac{8}{{28}} = \frac{{83}}{{28}}\)
Vậy:
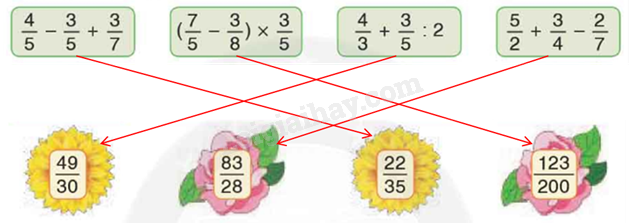
Câu 3
Trả lời câu hỏi 3 trang 30
a) Viết mỗi hỗn số sau thành phân số thập phân:
$63\frac{8}{{10}}$
$5\frac{{26}}{{1000}}$
b) Viết các phân số thập phân sau thành hỗn số:
$\frac{{276}}{{100}}$
$\frac{{7092}}{{1000}}$

a) Cách chuyển hỗn số thành phân số:
- Tử số của phân số mới bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số.
- Mẫu số bằng mẫu số ở phần phân số.
b) Cách chuyển phân số thập phân thành hỗn số:
- Lấy tử số chia cho mẫu số.
- Thương tìm được là phần nguyên; viết phần nguyên kèm theo một phân số có tử số là số dư, mẫu số là số chia.

a)
$63\frac{8}{{10}} = \frac{{63 \times 10 + 8}}{{10}} = \frac{{638}}{{10}}$
$5\frac{{26}}{{1000}} = \frac{{5 \times 1000 + 26}}{{1000}} = \frac{{5026}}{{1000}}$
b) Ta có: 276 : 100 = 2 (dư 76)
Vậy:
Advertisements (Quảng cáo)
$\frac{{276}}{{100}} = 2\frac{{76}}{{100}}$
Ta có: 7 092 : 1 000 = 7 (dư 92)
$\frac{{7092}}{{1000}} = 7\frac{{92}}{{1000}}$
Câu 4
Trả lời câu hỏi 4 trang 30
Trong ngày Quốc tế Thiếu nhi, một cửa hàng bán đồ chơi đã bán số búp bê bằng $\frac{3}{5}$ số siêu nhân và ít hơn số siêu nhân 8 con. Tìm số búp bê và số siêu nhân đã bán.

- Vẽ sơ đồ.
- Tìm số búp bê và số siêu nhân đã bán theo bài toán tìm hai số khi biết hiệu và tỉ số của hai số đó.

Ta có sơ đồ:
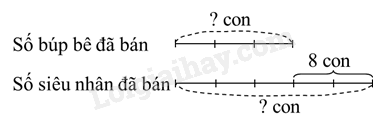
Theo sơ đồ, hiệu số phần bằng nhau là:
5 – 3 = 2 (phần)
Số búp bê đã bán là
8 : 2 x 3 = 12 (con)
Số siêu nhân đã bán là:
12 + 8 = 20 (con)
Đáp số: Búp bê: 12 con ; Siêu nhân: 20 con.
Câu 5
Trả lời câu hỏi 5 trang 30
Chọn câu trả lời đúng:
Bác Hai dựng nước trong hai thùng. Lượng nước chứa trong thùng thứ nhất bằng $\frac{5}{3}$ lượng nước trong thùng thứ hai. Sau khi chia đều lượng nước đó ở cả hai thùng thì mỗi thùng đều chứa 160 l nước. Vậy lúc đầu:
A. Thùng thứ nhất chứa 60 l nước và thùng thứ hai chứa 100 l nước.
B. Thùng thứ nhất chứa 200 l nước và thùng thứ hai chứa 120 l nước.
C. Thùng thứ nhất chứa 120 l nước và thùng thứ hai chứa 200 l nước.
D. Thùng thứ nhất chứa 100 l nước và thùng thứ hai chứa 60 l nước.

- Tổng số lít nước ở hai thùng lúc đầu = Tổng số lít nước ở hai thùng lúc sau.
- Đưa về bài toán tìm hai số khi biết tổng và tỉ số của hai số đó.

Tóm tắt
Lượng nước trong thùng thứ nhất: $\frac{5}{3}$ lượng nước trong thùng thứ hai
Sau khi chia đều, mỗi thùng chứa: 160 l nước
Ban đầu thùng thứ nhất: ? l nước
Thùng thứ hai: ? l nước
Bài giải
Vì khi chia đều lượng nước ở cả hai thùng nên tổng số lít nước ở hai thùng lúc đầu bằng tổng số lít nước ở hai thùng lúc sau.
Tổng số lít nước ở hai thùng lúc đầu là:
160 + 160 = 320 (lít)
Ta có sơ đồ:
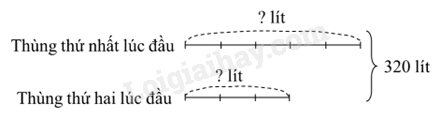
Theo sơ đồ, tổng số phần bằng nhau là:
5 + 3 = 8 (phần)
Lúc đầu thùng thứ nhất chứa số lít nước là:
320 : 8 x 5 = 200 (lít)
Lúc đầu thùng thứ hai chứa số lít nước là:
320 – 200 = 120 (lít)
Đáp số: Thùng thứ nhất: 200 l nước;
Thùng thứ hai: 120 l nước.
Chọn B.
