Câu 1
Trả lời câu hỏi 1 trang 46
Tính thể tích hình hộp chữ nhật có chiều dài a, chiều rộng b, chiều cao c:
a) a = 8 cm; b = 6 cm; c = 6 cm
b) a = 1,5 m; b = 0,8 m; c = 0,5 m
c) a = $\frac{5}{2}$ dm; b = 2 dm; c = 0,6 dm

Thể tích hình hộp chữ nhật: $V = a \times b \times c$

a) Thể tích hình hộp chữ nhật đó là:
$8 \times 6 \times 6 = 288$(cm3)
Đáp số: 288 cm3
b) Thể tích hình hộp chữ nhật đó là:
$1,5 \times 0,8 \times 0,5 = 0,6$(m3)
Đáp số: 0,6 m3
c) Thể tích hình hộp chữ nhật đó là:
$\frac{5}{2} \times 2 \times 0,6 = 3$(dm3)
Đáp số: 3 dm3.
Câu 2
Trả lời câu hỏi 2 trang 46
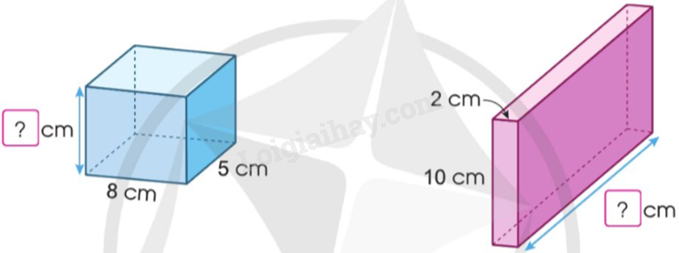
Mỗi hình hộp sau đều có thể tích 280 cm3. Tìm độ dài cạnh còn lại:

Thể tích hình hộp chữ nhật: $V = a \times b \times c$
Nên suy ra: $c = V:\left( {a \times b} \right)$và $a = V:\left( {b \times c} \right)$

Độ dài cạnh còn lại của hình thứ nhất là:
$280:\left( {8 \times 5} \right) = 7$(cm)
Độ dài cạnh còn lại của hình thứ hai là:
$280:\left( {10 \times 2} \right) = 14$(cm)
Đáp số: 7 cm; 14 cm.
Câu 3
Trả lời câu hỏi 3 trang 46
Một khối đá có dạng hình hộp chữ nhật với chiều dài 2,5 m, chiều rộng 1,6m và chiều cao 1,2 m.
a) Tính thể tích khối đá đó.
b) Theo em, nếu mỗi mét khối đá nặng 2,7 tấn thì xe tải 15 tấn có chở được khối đá đó không?

a) Tính thể tích khối đá = chiều dài $ \times $ chiều rộng $ \times $ chiều cao
b) Tính cân nặng của khối đá = cân nặng 1 m3 đá x thể tích khối đá.
So sánh cân nặng của khối đá với cân nặng xe tải.

a) Thể tích khối đá đó là:
$2,5 \times 1,6 \times 1,2 = 4,8$(m3)
b) Khối đá đó cân nặng số tấn là:
$4,8 \times 2,7 = 12,96$(tấn)
Vì 12,96 < 15 Nên cân nặng của khối đá < cân nặng xe tải
Vậy xe tải 15 tấn có chở được khối đá đó.
Đáp số: a) 4,8 m3;
b) Có.
Câu 4
Trả lời câu hỏi 4 trang 46
Tính thể tích của mỗi hình sau:
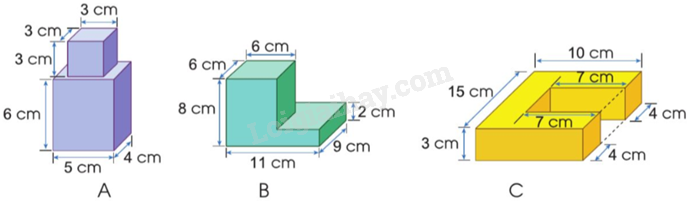

Chia các hình vẽ thành các hình nhỏ rồi tính thể tích từng hình theo công thức $V = a \times b \times c$ hoặc $V = a \times a \times a$, từ đó suy ra thể tích hình vẽ ban đầu.

a) Chia hình A thành 2 hình như hình dưới đây:
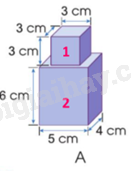
Thể tích hình 1 là:
$3 \times 3 \times 3 = 27$(cm3)
Thể tích hình 2 là:
$6 \times 5 \times 4 = 120$(cm3)
Thể tích hình A là:
27 + 120 = 147 (cm3)
Đáp số: 147 cm3
b) Chia hình B thành 2 hình như hình dưới đây:
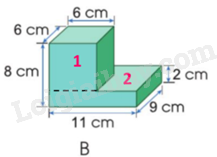
Thể tích hình 1 là:
$6 \times 6 \times \left( {8 - 2} \right) = 216$(cm3)
Thể tích hình 2 là:
$11 \times 9 \times 2 = 198$(cm3)
Thể tích hình B là:
Advertisements (Quảng cáo)
216 + 198 = 414 (cm3)
Đáp số: 414 cm3
c) Chia hình C thành 3 hình như hình dưới đây:
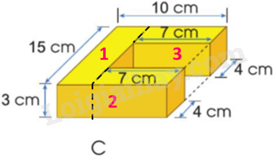
Thể tích hình 1 là:
$15 \times 3 \times \left( {10 - 7} \right) = 135$(cm3)
Thể tích hình 2 là:
$3 \times 4 \times 7 = 84$(cm3)
Thể tích hình 3 là:
$3 \times 4 \times 7 = 84$(cm3)
Thể tích hình C là:
135 + 84 + 84 = 303 (cm3)
Đáp số: 303 cm3
Câu 5
Trả lời câu hỏi 5 trang 47
Quan sát hình vẽ.
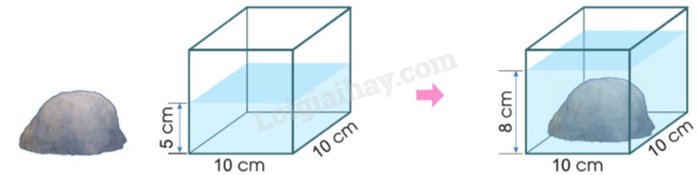
a) Tính thể tích viên đá:
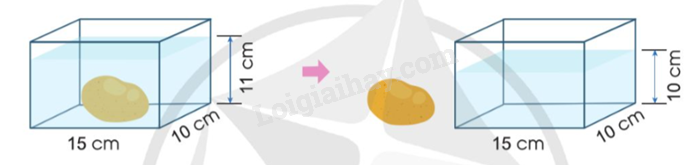
b) Tính thể tích củ khoai tây:
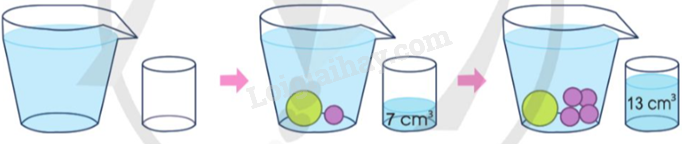
c) Đặt các câu hỏi liên quan đến thể tích

a) Cách 1: Thể tích viên đá = Tổng thể tích viên đá và nước – thể tích nước trong bể
Cách 2: Thể tích của viên đá bằng thể tích của hình hộp chữ nhật (phần nước dâng lên) có chiều dài 10 cm, chiều rộng 10 cm và chiều cao là: 8 – 5 = 3 (cm).
b) Tương tự như phần a.
c) Đặt các câu hỏi liên quan đến thể tích

a) Cách 1:
Thể tích nước trong bể là:
$10 \times 10 \times 5 = 500$(cm3)
Tổng thể tích viên đá và nước là:
$10 \times 10 \times 8 = 800$(cm3)
Thể tích viên đá là:
800 – 500 = 300 (cm3)
Cách 2:
Chiều cao của phần nước dâng lên là:
8 – 5 = 3 (cm)
Thể tích nước dâng lên là:
$10 \times 10 \times 3 = 300$(cm3)
Thể tích nước dâng lên chính là thể tích viên đá.
b)
Chiều cao của phần nước dâng lên là:
10 – 11 = 1 (cm)
Thể tích nước dâng lên là:
$15 \times 10 \times 1 = 150$(cm3)
Thể tích nước dâng lên chính là thể tích củ khoai tây.
c) Ví dụ: Cho một vật vào bình nước chứa đầy nước, tính thể tích của vật đó như thế nào?
Thể tích của quả bóng màu xanh và 1 quả bóng màu tím là bao nhiêu?
Thể tích của quả bóng màu xanh và 4 quả bóng màu tím là bao nhiêu?
Thể tích của quả bóng màu xanh là bao nhiêu?
Thể tích của 3 quả bóng màu tím là bao nhiêu?
Thể tích của 1 quả bóng màu tím là bao nhiêu?
Câu 6
Trả lời câu hỏi 6 trang 47
Thùng xăng của một ô tô tải có dạng hình hộp chữ nhật với chiều dài 7 dm, chiều rộng 4 dm và chiều cao 2 dm.
a) Hỏi thùng xăng đó có thể chứa tối đa bao nhiêu lít xăng?
b) Giá bán mỗi lít xăng là 22 600 đồng. Hỏi muốn đổ đầy thùng xăng đó cần trả bao nhiêu tiền?

a) Tính thể tích thùng xăng: $V = a \times b \times c$
Dựa vào mối quan hệ: 1 dm3 =1 l để suy ra số lít xăng tối đa thùng xăng đó có thể chứa.
b) Tính số tiền phải trả để đổ đầy thùng xăng = Giá bán mỗi lít xăng $ \times $ số lít xăng tối đa thùng xăng đó chứa

a) Thể tích thùng xăng đó là:
$7 \times 4 \times 2 = 56$(dm3)
Vì 1 dm3 = 1 l nên thùng xăng đó có thể chứa tối đa 56 lít xăng.
b) Muốn đổ đầy thùng xăng đó cần trả số tiền là:
$56 \times 22600 = 1265600$(đồng)
Đáp số: a) 56 l xăng;
b) 1 265 600 đồng.
