Câu 1
Có thể, chắc chắn hay không thể?
Khi tung một đồng tiền xu:

a) Sự kiện mặt sấp xuất hiện .?. xảy ra.
Sự kiện mặt ngửa xuất hiện .?. xảy ra.
Như vậy, có hai khả năng xảy ra.
b) .?. xảy ra một trong hai sự kiện: mặt sấp xuất hiện hay mặt ngửa xuất hiện.
c) .?. đồng thời xảy ra hai sự kiện: mặt sấp xuất hiện và mặt ngửa cũng xuất hiện.

Điền từ thích hợp vào chỗ chấm.

a) Sự kiện mặt sấp xuất hiện có thể xảy ra.
Sự kiện mặt ngửa xuất hiện có thể xảy ra.
Như vậy, có hai khả năng xảy ra.
b) Chắc chắn xảy ra một trong hai sự kiện: mặt sấp xuất hiện hay mặt ngửa xuất hiện.
c) Không thể đồng thời xảy ra hai sự kiện: mặt sấp xuất hiện và mặt ngửa cũng xuất hiện.
Câu 2
Vinh tung nhiều lần liên tiếp một đồng xu. Dưới đây là bảng kết quả kiểm đếm và ghi chép số lần xuất hiện các mặt của đồng xu.

a) Vinh đã tung đồng xu tất cả bao nhiêu lần?
b) Viết tỉ số của số lần xảy ra sự kiện mặt sấp xuất hiện và tổng số lần tung.

Quan sát bảng và trả lời câu hỏi.

a) Số lần xảy ra sự kiện mặt sấp là 23 lần
Số lần xảy ra sự kiện mặt ngửa là 32 lần
Số lần Vinh đã tung đồng xu là:
23 + 32 = 55 (lần)
b) Tỉ số của số lần xảy ra sự kiện mặt sấp xuất hiện và tổng số lần tung là: 23 : 55 = $\frac{{23}}{{55}}$
Câu 3
Advertisements (Quảng cáo)
Một cầu thủ thực hiện 100 lần ném bóng. Số lần bóng vào rổ bằng $\frac{3}{2}$ số lần bóng không vào rổ. Hỏi cầu thủ đó đã ném bóng vào rổ bao nhiêu lần?

- Vẽ sơ đồ
- Tìm tổng số phần bằng nhau
- Tìm giá trị của một phần
- Tìm số lần cầu thủ đã ném bóng vào rổ

Theo đề bài, ta có sơ đồ:
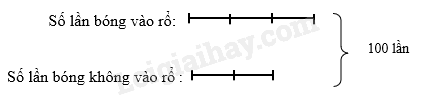
Theo sơ đồ, tổng số phần bằng nhau là:
3 + 2 = 5 (phần)
Giá trị của một phần là:
100 : 5 = 20
Cầu thủ đã ném bóng vào rổ số lần là:
20 x 3 = 60 (lần)
Đáp số: 60 lần
Câu 4
Một hộp đựng hai loại tất chỉ khác nhau về màu sắc (xem hình). Không nhìn vào hộp, cần lấy ra ít nhất bao nhiêu chiếc tất để chắc chắn có một đôi tất cùng màu?


Quan sát hình và trả lời câu hỏi.

Không nhìn vào hộp, cần lấy ra ít nhất 3 chiếc tất để chắc chắn có một đôi tất cùng màu.
Trong hộp có 6 chiếc tất màu xanh và 4 chiếc tất màu đỏ. Khi lấy 3 chiếc tất, có các trường hợp có thể xảy ra là: 3 chiếc tất màu xanh, 3 chiếc tất màu đỏ, 2 chiếc tất màu đỏ và 1 chiếc tất màu xanh, 2 chiếc tất màu xanh và 1 chiếc tất màu đỏ. Vậy chắc chắn lấy được 1 đôi tất cùng màu.
Vui học
Hai bạn chơi oẳn tù tì. Mỗi lần, bạn nào thắng thì bạn đó được vẽ một vạch. Sau 15 lần chơi, mỗi bạn viết tỉ số của số lần thắng và tổng số lần chơi. Bạn nào có tỉ số lớn hơn là người thắng.

Tỉ số lần thắng và tổng số lần chơi = số lần thắng : tổng số lần chơi

- HS chơi oẳn tù tì và ghi lại kết quả
- Tỉ số lần thắng và tổng số lần chơi = số lần thắng : tổng số lần chơi
