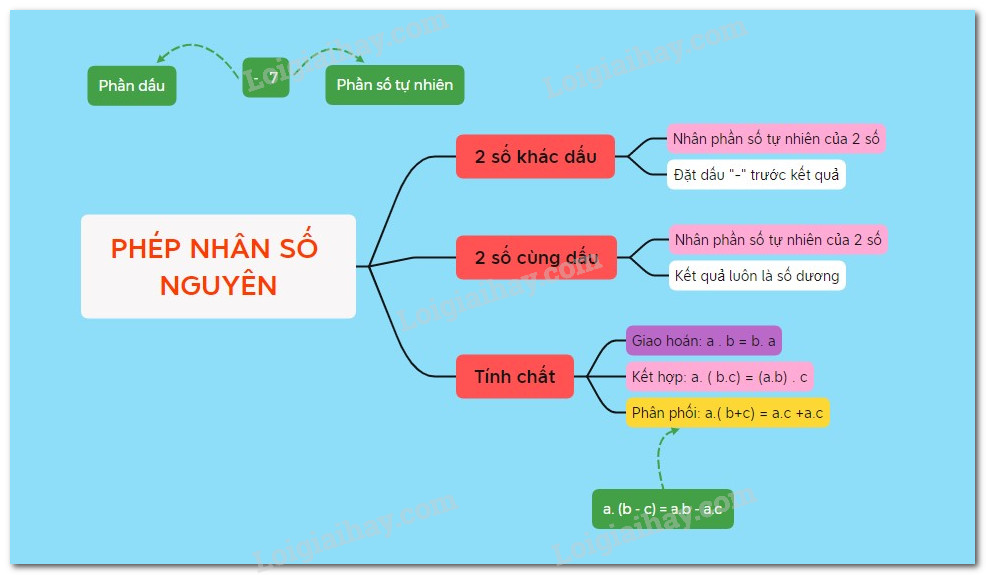
1. Qui tắc nhân hai số nguyên khác dấu
Muốn nhân hai số nguyên khác dấu, ta nhân phần số tự nhiên của chúng rồi đặt dấu “-” trước kết quả nhận được.
Ví dụ:
\(5.( - 5) = - 25\)
\(\begin{array}{l}\left( { - 5} \right).9 = - \left( {5.9} \right) = - 45\\3.\left( { - 3} \right) = - \left( {3.3} \right) = - 9\\\left( { - 6} \right).0 = 0\end{array}\)
Chú ý:
+) \(a.0 = 0\)
+) Cách nhận biết dấu của tích:
\(\left( + \right).\left( + \right)\) \( \to \left( + \right)\)
\(\left( - \right).\left( - \right) \to \left( + \right)\)
\(\left( + \right).\left( - \right) \to \left( - \right)\)
\(\left( - \right).\left( + \right) \to \left( - \right)\)
+) \(a.b = 0\) thì \(a = 0\) hoặc \(b = 0\)
+) Khi đổi dấu một thừa số thì tích đổi dấu. Khi đổi dấu hai thừa số thì tích không thay đổi.
+) \(\left( { - a} \right).a = a.\left( { - a} \right) = - {a^2}\)
2.Qui tắc nhân hai số nguyên cùng dấu
Muốn nhân hai số nguyên cùng dấu, ta nhân phần số tự nhiên của chúng rồi đặt dấu “+” trước kết quả của chúng.
Ví dụ: \(( - 5).\left( { - 6} \right) = 5.6 = 30\)
+ Nhân hai số nguyên dương nghĩa là nhân hai số tự nhiên khác \(0.\)
+ Nhân hai số nguyên âm ta nhân phần số tự nhiên của chúng.
Nhận xét: Tích của hai số nguyên âm là một số nguyên dương
Advertisements (Quảng cáo)
Chú ý:
+) \(a.0 = 0.a = 0\)
+) \(a.b = 0\) thì \(a = 0\) hoặc \(b = 0.\)
3.Tính chất của phép nhân
Giao hoán: \(a.b = b.a\)
Kết hợp: \(\left( {a.b} \right).c = a.\left( {b.c} \right)\)
Nhân với số \(1:\) \(a.1 = 1.a = a\)
Tính chất phân phối của phép nhân đối với phép cộng: \(a.\left( {b + c} \right) = ab + ac\)
Tính chất trên cũng đúng đối với phép trừ: \[a\left( {b - c} \right) = ab - ac\]
Ví dụ:
Thực hiện phép tính:
a) \(\left( { - 12} \right).3.\left( { - 5} \right)\)
\(\begin{array}{l}\left( { - 12} \right).3.\left( { - 5} \right) = \left( { - 12} \right).\left( { - 5} \right).3\\ = \left[ {\left( { - 12} \right).\left( { - 5} \right)} \right].3 = \left( {12.5} \right).3\\ = 60.3 = 180\end{array}\)
b) \(\left( { - 3} \right).\left( {100 - 2} \right)\)
\(\begin{array}{l}\left( { - 3} \right).\left( {100 - 2} \right) = \left[ {\left( { - 3} \right).100} \right] - \left[ {\left( { - 3} \right).2} \right]\\ = \left( { - 3} \right).100 - \left[ { - \left( {3.2} \right)} \right]\\ = - \left( {3.100} \right) - \left( { - 6} \right)\\ = - 300 + 6 = - \left( {300 - 6} \right) = - 294\end{array}\)
Chú ý:
+ Nhờ tính chất kết hợp ta có tích của ba, bốn, năm… số nguyên.
+ Khi thực hiện phép nhân nhiều số nguyên, ta có thể dựa vào các tính chất giao hoán và kết hợp để thay đổi vị trí giữa các thừa số, đặt dấu ngoặc để nhóm các thừa số thích hợp.
+ Tích của \(n\) số nguyên \(a\) là lũy thừa bậc \(n\) của số nguyên \(a.\)